设D是周线C的内部 f(z)在闭域=D+C上解析．试证：在D内不可能存在一点z0使 ｜f(z)｜＜｜
设D是周线C的内部，f(z)在闭域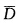
=D+C上解析．试证：在D内不可能存在一点z0使 ｜f(z)｜＜｜f(z0)｜ (z∈C)．
请帮忙给出正确答案和分析，谢谢！
参考解答
432***102
2024-11-21 00:21:06
正确答案：(反证法)应用儒歇定理考虑一f(z0)与f(z)一f(z0)．假设成立则对一f(z0)f(z)一f(z0)用儒歇定理一f(z0)与f(z)一f(z0)在D内有相同零点个数而f(z)一f(z0)在D内至少有一个零点因而一f(z0)在D内亦应至少有一个零点此显然不可能矛盾．假设不成立．
(反证法)应用儒歇定理,考虑一f(z0)与f(z)一f(z0)．假设成立,则对一f(z0),f(z)一f(z0)用儒歇定理,一f(z0)与f(z)一f(z0)在D内有相同零点个数,而f(z)一f(z0)在D内至少有一个零点,因而一f(z0)在D内亦应至少有一个零点,此显然不可能,矛盾．假设不成立．
相似问题
证明：函数z－2是函数 证明 f(z)==z＋z2＋z6＋…＋zn!＋… 以单位圆周｜z｜=1为自然
证明：函数z－2是函数 证明 f(z)==z＋z2＋z6＋…＋zn!＋… 以单位圆周｜z｜=1为自然边界．证明 f(z)==z+z2+z6+…+zn!+… 以单位圆周｜z｜=1为自然边
如果单叶解析函数w=f(z)把z平面上可求面积的区域D共形映射成w平面上的区域G 试证G的面积 A=
如果单叶解析函数w=f(z)把z平面上可求面积的区域D共形映射成w平面上的区域G，试证G的面积 A=｜f(z)｜2dxdy，(z=x+iy)．请帮忙给出正确答案和分析，谢谢！
设函数w=f(z)在｜z｜＜1内解析 且是将｜z｜＜1共形映射成｜w｜＜1的分式线性变换．试证 问线
设函数w=f(z)在｜z｜＜1内解析，且是将｜z｜＜1共形映射成｜w｜＜1的分式线性变换．试证 问线性变换w=将闭问线性变换w=将闭单位圆｜z｜≤1映成w平面上的
将下列函数在指定环域内展为洛朗级数． 将下列各函数在指定点的去心邻域内展成洛朗级数 并指出其将下列各
将下列函数在指定环域内展为洛朗级数． 将下列各函数在指定点的去心邻域内展成洛朗级数，并指出其将下列各函数在指定点的去心邻域内展成洛朗级数，并指
盒中装有10只外形相同的晶体管 其中4只次品 6只正品。现从中随机抽取一只测试 测试后不放回 直到找
盒中装有10只外形相同的晶体管，其中4只次品，6只正品。现从中随机抽取一只测试，测试后不放回，直到找出4只次品为止，求最后一只次品晶体管在第10次测试
