设A是n阶实矩阵．证明：存在正交矩阵Q使Q－1AQ为三角矩阵的充要条件是A的特征值全为实数．请帮忙给

正确答案：为确定起见这里三角矩阵不妨设为上三角矩阵． 先证必要性．不妨设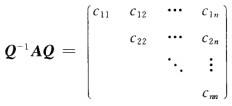其中QA均为实矩阵从而C_ij都是实数．又因为相似矩阵有相同的特征多项式所以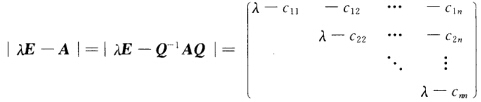=(λ－C₁₁)(λ－C₂₂)…(λ－C_nn)．从而A的n个特征值C₁₁C₂₂…C_nn均为实数． 再证充分性．设λ₁λ₂…λ_n为A的所有不同的实特征值则A与某一Jordan形矩阵J相似即存在可逆实矩阵P₀使P₀^－1AP₀=J其中且由于λ_i都是实数所以J为上三角实矩阵． 另一方面矩阵P₀可以分解为P₁=Q₀S₀．其中Q₀是正交矩阵s₀为上三角矩阵于是P₀¹AP₀=S₀^－1Q₀^－1AQ₀Js₀^－1即Q₀^－1AQ₀=S₀JS₀^－1．由于S₀JS₀^－1都是上三角矩阵因而它们的积也为上三角矩阵即充分性得证．
为确定起见,这里三角矩阵不妨设为上三角矩阵．先证必要性．不妨设其中Q,A均为实矩阵,从而Cij都是实数．又因为相似矩阵有相同的特征多项式,所以=(λ－C11)(λ－C22)…(λ－Cnn)．从而A的n个特征值C11,C22,…,Cnn均为实数．再证充分性．设λ1,λ2,…,λn为A的所有不同的实特征值,则A与某一Jordan形矩阵J相似,即存在可逆实矩阵P0,使P0－1AP0=J,其中且由于λi都是实数,所以J为上三角实矩阵．另一方面,矩阵P0可以分解为P1=Q0S0．其中Q0是正交矩阵,s0为上三角矩阵,于是P01AP0=S0－1Q0－1AQ0Js0－1,即Q0－1AQ0=S0JS0－1．由于S0,J,,S0－1都是上三角矩阵,因而它们的积也为上三角矩阵,即充分性得证．