设α1 α2 … αn是互不相同的n个数 且fi=(x－α1)…(x－αi－1)(x－αi+1)…(

正确答案：(1)由题意只需证f₁(x)f₂(x)…f_n(x)线性无关即可．现假设k₁f₁(x)+k₂f₂(x)+…+k_nf_n(x)=0．分别以x=α_i代入上式得到k_if_i(α_i)=0．因为f₁(α_i)≠0故k_i=0i=12…n．由此可得f₁(x)f₂(x)…f_n(x)线性无关．又因为dim P[x_n=n可知f₁(x)f₂(x)…f_n(x)为P[x_n的基． (2)取全部n次单位根为α₁=ε₁α₂=ε₂…α_n=ε_n则x_n－1=(x－ε₁)(x－ε₂)…(x一ε_n)=(x－ε_i)f_n(x)i=12…n．于是可得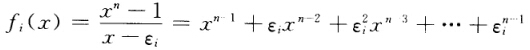故所求过渡矩阵为
(1)由题意,只需证f1(x),f2(x),…,fn(x)线性无关即可．现假设k1f1(x)+k2f2(x)+…+knfn(x)=0．分别以x=αi代入上式,得到kifi(αi)=0．因为f1(αi)≠0,故ki=0,i=1,2,…,n．由此可得f1(x),f2(x),…,fn(x)线性无关．又因为dimP[xn,=n,可知f1(x),f2(x),…,fn(x)为P[xn的基．(2)取全部n次单位根为α1=ε1,α2=ε2,…,αn=εn,则xn－1=(x－ε1)(x－ε2)…(x一εn)=(x－εi)fn(x),i=1,2,…,n．于是可得故所求过渡矩阵为