首页大学本科正文

设A与B均为n阶实对称矩阵 且B为正定矩阵 A－B为半正定矩阵 证明：∣A∣－∣B∣≥0．请帮忙给出

大学本科 已帮助：人 时间:2024-11-12 04:24:24

设A与B均为n阶实对称矩阵，且B为正定矩阵，A－B为半正定矩阵，证明：∣A∣－∣B∣≥0．
请帮忙给出正确答案和分析，谢谢！

#站内搜索 #在百度搜 #在搜狗搜

难度：⭐⭐⭐

题库：大学本科,理学,数学类

标签：正定,均为,矩阵

参考解答

用户头像

473***101

2024-11-12 04:24:24

正确答案：由于B为正定的A－B为半正定的则存在可逆矩阵P1使P1TBP1=E且P1T(A－B)P1也是对称的故存在正交矩阵Q使得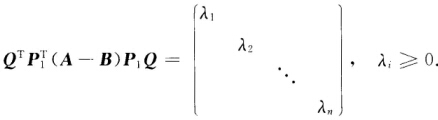取P=P1Q则P可逆且∣PT∣(∣B∣+∣A－B∣)∣P∣=∣PTBP∣+∣PT(A—B)P∣－1+λ1λ2…λn．从而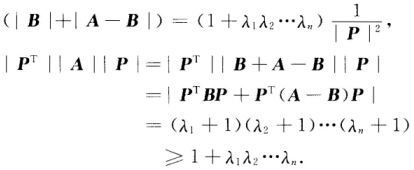因此∣A∣≥(λ1λ2…λn)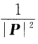故(∣B∣+∣A－B∣)≤∣A∣从而∣A－B∣≤∣A∣－∣B∣又因为A－B为半正定的所以∣A—B∣≥0故∣A∣－∣B∣≥0．
由于B为正定的,A－B为半正定的,则存在可逆矩阵P1,使P1TBP1=E,且P1T(A－B)P1也是对称的,故存在正交矩阵Q,使得取P=P1Q,则P可逆,且∣PT∣(∣B∣+∣A－B∣)∣P∣=∣PTBP∣+∣PT(A—B)P∣－1+λ1λ2…λn．从而因此∣A∣≥(λ1λ2…λn),故(∣B∣+∣A－B∣)≤∣A∣,从而∣A－B∣≤∣A∣－∣B∣,又因为A－B为半正定的,所以∣A—B∣≥0,故∣A∣－∣B∣≥0．

上一篇 设随机变量X的分布函数为设连续型随机变量X的分布函数是试确定A及B的值 并求相应的概率密度函数f设连

下一篇 设随机变量X的分布函数为设离散型随机变量X的可能取值为x1=一1 x2=0 x3=1 且E(X)=0

相似问题