某大学数学测验 抽得20个学生的分数平均数要求一种元件平均使用寿命不得低于1 000小时 生产者从要
某大学数学测验，抽得20个学生的分数平均数要求一种元件平均使用寿命不得低于1 000小时，生产者从
要求一种元件平均使用寿命不得低于1 000小时，生产者从一批这种元件中随机抽取25件，测得其寿命的平均值为950小时．已知该种元件寿命服从标准差为σ=100小时的正态分布，试在显著性水平a=0．05下确定这批元件是否合格?设总体均值为μ，μ未知，即需检验假设H0：λ≥1 000，H1：μ＜1 000．
请帮忙给出正确答案和分析，谢谢！
参考解答
473***101
2024-11-12 05:40:05
正确答案：检验假设H0：u≥1000H1：μ＜1000．这是单边假设检验问题．由于方差σ2=1002故用u检验法．对于显著性水平a=0．05拒绝域为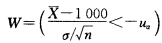
查标准正态分布表得u0.05=1．645．又知n=25
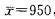故可计算出样本值
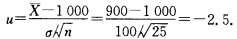因为一2．5＜一1．645故在a=0．05下拒绝H0即认为这批元件不合格．
检验假设H0：u≥1000,H1：μ＜1000．这是单边假设检验问题．由于方差σ2=1002,故用u检验法．对于显著性水平a=0．05,拒绝域为查标准正态分布表,得u0.05=1．645．又知n=25,故可计算出样本值因为一2．5＜一1．645,故在a=0．05下拒绝H0,即认为这批元件不合格．
相似问题
设总体X～N(μ σ2) X1 X2 … Xn为来自总体X的样本 当用从一台车床加工的成批轴料中抽取
设总体X～N(μ，σ2)，X1，X2，…，Xn为来自总体X的样本，当用从一台车床加工的成批轴料中抽取15件测量其椭从一台车床加工的成批轴料中抽取15件测量其椭
设ξ η是相互独立的 且概率密度分别为一袋中装有5只球 编号为1 2 3 4 5．在袋中同时取3只
设ξ，η是相互独立的，且概率密度分别为一袋中装有5只球，编号为1，2，3，4，5．在袋中同时取3只，以X表示一袋中装有5只球，编号为1，2，3，4，5．在袋
设总体X的数学期望为μ X1 X2 … Xn是来自X的样本 a1 a2 … an是任意常数 验证设X
设总体X的数学期望为μ，X1，X2，…，Xn是来自X的样本，a1，a2，…，an是任意常数，验证设X1，X2，…，Xn为来自参设X1，X2，…，Xn为来自参数为n，P的二
设总体X～N(μ σ2) X1 X2 … Xn为来自总体X的样本 当用当取得一组样本值x1 x2 …
设总体X～N(μ，σ2)，X1，X2，…，Xn为来自总体X的样本，当用当取得一组样本值x1，x2，…，xn时，记c1=θ(x1，…，x当取得一组样本值x1，x2，…，xn时，
已知总体X服从[0 λ]上的均匀分布(λ未知) X1 X2 … Xn为X的样本 则( )．A．是一个
已知总体X服从[0，λ]上的均匀分布(λ未知)，X1，X2，…，Xn为X的样本，则( )．A．是一个统计量；B．是一个统计量；C．X1+X2是一个统计量；D．是一个统
