设g(x)=∫0xf(u)du 其中则g(x)在区间(0 2)内A.无界.B.递减.C.不连续.D.
设g(x)=∫0xf(u)du,其中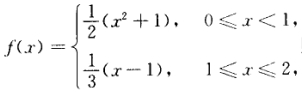 则g(x)在区间(0,2)内
则g(x)在区间(0,2)内
A.无界.
B.递减.
C.不连续.
D.连续.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:D
相似问题
设在闭区间[a b]上f(x)>0 f(x)<0 f'(x)>0.记S1=∫ab(x)dx S2=f
设在闭区间[a,b]上f(x)>0,f(x)<0,f"(x)>0.记S1=∫ab(x)dx,S2=f(b)(b-a),S3=,则A.S1<S2<S3.B.S2<S3<S1.C.S3<S1<S2.D.S2<S1<
设函数f(x)在(0 +∞)内连续 且对所有x t∈(0 +∞) 满足条件∫1xtf(u)du=t
设函数f(x)在(0,+∞)内连续,,且对所有x,t∈(0,+∞),满足条件∫1xtf(u)du=t∫xxf(u)du+x∫1tf(u)du,求f(x).请帮忙给出正确答案和分析,谢谢!
设f(x) g(x)在[a b]上连续 且g(x)>0.利用闭区间上连续函数的性质 证明:存在一点ξ
设f(x),g(x)在[a,b]上连续,且g(x)>0.利用闭区间上连续函数的性质,证明:存在一点ξ∈[a,b],使∫abf(x)g(x)=f(ξ)∫abg(x)dx.请帮忙给出正确答案和分析,谢谢!
设函数f(x)在闭区间[a b]上连续 在开区间(a b)内可导 且f(x)>0.若极限存在 证明:
设函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(x)>0.若极限存在,证明: (1)在(a,b)内f(x)>0; (2)在(a,b)内存在点ξ,使; (3)在
设D1是由抛物线y=2x2和直线x=a x=2及y=0所围成的平面区域;D2是由抛物线y=2x2和直
设D1是由抛物线y=2x2和直线x=a,x=2及y=0所围成的平面区域;D2是由抛物线y=2x2和直线y=0,x=a所围成的平面区域,其中0<a<2. (1)试求D1绕x轴旋












