设φ(u v)=常数 φ(u v)=常数为曲面M上的两族正则曲线．证明：两族曲线正交对于正螺面M：x
设φ(u，v)=常数，φ(u，v)=常数为曲面M上的两族正则曲线．证明：两族曲线正交对于正螺面M：x(u，v)=(vcos
对于正螺面M：x(u，v)=(vcosu，vsinu，bu) (一∞<u，v<+∞，b>0)，处处有LG一2FM+EN=0．
请帮忙给出正确答案和分析，谢谢！
参考解答
473***102
2024-11-17 02:25:00
正确答案：由例2．7．8知E=v2+b2 F=0 G=1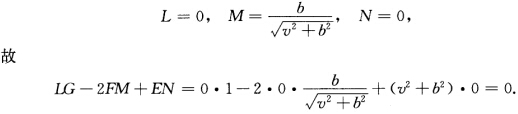
这正表明正螺面M为极小曲面即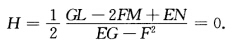
由例2．7．8,知E=v2+b2,F=0,G=1,这正表明正螺面M为极小曲面,即
相似问题
R3中k≠0 τ≠0的C4连通曲线x(s)为球面曲线等价于证明：曲线与为Bertrand侣线．证明：
R3中k≠0，τ≠0的C4连通曲线x(s)为球面曲线等价于证明：曲线与为Bertrand侣线．证明：曲线与为Bertrand侣线．请帮忙给出正确答案和分析，谢谢！
若曲面在某一参数表示下 E F G为常数(E>0 G>0 EG—F2>0) 证明：该曲面是可展的．请
若曲面在某一参数表示下，E，F，G为常数(E>0，G>0，EG—F2>0)，证明：该曲面是可展的．请帮忙给出正确答案和分析，谢谢！
证明：曲面M：为可展曲面．请帮忙给出正确答案和分析 谢谢！
证明：曲面M：为可展曲面．请帮忙给出正确答案和分析，谢谢！
平面上取极坐标时 第1基本形式为I=dr2+rdθ2计算Fijk．请帮忙给出正确答案和分析 谢谢！
平面上取极坐标时，第1基本形式为I=dr2+rdθ2计算Fijk．请帮忙给出正确答案和分析，谢谢！
证明：任何两个正交方向的法曲率kn1 kn2之和kn1+kn2为常数．请帮忙给出正确答案和分析 谢谢
证明：任何两个正交方向的法曲率kn1，kn2之和kn1+kn2为常数．请帮忙给出正确答案和分析，谢谢！
