设方阵A满足A2一A一2E=O 证明A及A+2E都可逆 并求它们的逆矩阵请帮忙给出正确答案和分析 谢
设方阵A满足A2一A一2E=O,证明A及A+2E都可逆,并求它们的逆矩阵
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:先证A可逆由原式得A(A—E)=2E即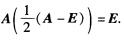 由方阵可逆的充要条件知A是可逆的且
由方阵可逆的充要条件知A是可逆的且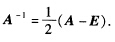 再证A+2E可逆.由(A+2E)(A一3E)=A2一A一6E=2E一6E=一4E即(A+2E)
再证A+2E可逆.由(A+2E)(A一3E)=A2一A一6E=2E一6E=一4E即(A+2E)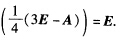 知A+2E可逆且(A+2E)-1=
知A+2E可逆且(A+2E)-1=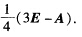
先证A可逆,由原式得A(A—E)=2E,即由方阵可逆的充要条件知A是可逆的,且再证A+2E可逆.由(A+2E)(A一3E)=A2一A一6E=2E一6E=一4E,即(A+2E)知A+2E可逆,且(A+2E)-1=
相似问题
已知3阶矩阵A可逆 将A的第2列与第3列交换得B 再把B的第1列的一2倍加到第3列得C 则满足PA-
已知3阶矩阵A可逆,将A的第2列与第3列交换得B,再把B的第1列的一2倍加到第3列得C,则满足PA-1=C-1的矩阵P为_____ A. B. C. D. 请帮忙给出正确答案和分析,谢谢!
设非负矩阵A∈Rn×n 若A有正特征向量x 则对所有m=1 2 …和i=1 2 … n 有 其中
设非负矩阵A∈Rn×n,若A有正特征向量x,则对所有m=1,2,…和i=1,2,…,n,有 ,其中Am=(ij(m)).特别地,若γ(A)>0,则对m=1,2,…,都有γ(A)-
设A为列满秩矩阵 AB=C 证明线性方程Bx=0与Cx=0同解.请帮忙给出正确答案和分析 谢谢!
设A为列满秩矩阵,AB=C,证明线性方程Bx=0与Cx=0同解.请帮忙给出正确答案和分析,谢谢!
设四元线性方程组(Ⅰ)为又已知齐次线性方程组(Ⅱ)的通解为k1(0 1 1 0)T+k2(一1 2
设四元线性方程组(Ⅰ)为又已知齐次线性方程组(Ⅱ)的通解为k1(0,1,1,0)T+k2(一1,2,2,1)T. (1)求方程组(Ⅰ)的基础解系. (2)问线性方程组(Ⅰ)和(
某海事法院根据当事人甲进出口公司的请求 对承运其进口货物的乙海运公司所属的某船舶的航海日志予以复制。
某海事法院根据当事人甲进出口公司的请求,对承运其进口货物的乙海运公司所属的某船舶的航海日志予以复制。这一强制措施属于( )A、简易程序B、督促程序C












