设非负矩阵A∈Rn×n 若A有正特征向量x 则对所有m=1 2 …和i=1 2 … n 有 其中
设非负矩阵A∈Rn×n，若A有正特征向量x，则对所有m=1，2，…和i=1，2，…，n，有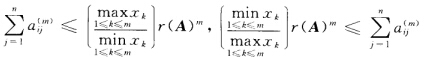 
，其中Am=(ij(m))．特别地，若γ(A)>0，则对m=1，2，…，都有γ(A)－1Am的各元一致有界．
请帮忙给出正确答案和分析，谢谢！
参考解答
413***101
2024-11-11 14:08:58
正确答案：若Ax=γ(A)x则Amx=γ(A)mx．若A≥0则Am≥0且有(γ(A))m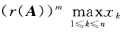
≥γ(Am)xi=(Amx)i=
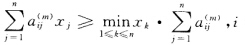=12…n．由于x>0两边同除以
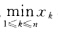即得结论．类似地有
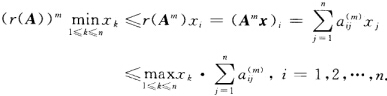再由x>0两边同除以
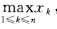即得结论．
若Ax=γ(A)x,则Amx=γ(A)mx．若A≥0,则Am≥0,且有(γ(A))m≥γ(Am)xi=(Amx)i==1,2,…,n．由于x>0,两边同除以,即得结论．类似地,有再由x>0,两边同除以,即得结论．
相似问题
设A为列满秩矩阵 AB=C 证明线性方程Bx=0与Cx=0同解．请帮忙给出正确答案和分析 谢谢！
设A为列满秩矩阵，AB=C，证明线性方程Bx=0与Cx=0同解．请帮忙给出正确答案和分析，谢谢！
设四元线性方程组(Ⅰ)为又已知齐次线性方程组(Ⅱ)的通解为k1(0 1 1 0)T+k2(一1 2
设四元线性方程组(Ⅰ)为又已知齐次线性方程组(Ⅱ)的通解为k1(0，1，1，0)T+k2(一1，2，2，1)T． (1)求方程组(Ⅰ)的基础解系． (2)问线性方程组(Ⅰ)和(
某海事法院根据当事人甲进出口公司的请求 对承运其进口货物的乙海运公司所属的某船舶的航海日志予以复制。
某海事法院根据当事人甲进出口公司的请求，对承运其进口货物的乙海运公司所属的某船舶的航海日志予以复制。这一强制措施属于( )A、简易程序B、督促程序C
已知线性方程组 (1)a b为何值时 方程组有解? (2)方程组有解时 求出其导出组的一个基础解系
已知线性方程组 (1)a，b为何值时，方程组有解? (2)方程组有解时，求出其导出组的一个基础解系． (3)方程组有解时，求出方程组的全部解．请帮忙给出
λ取何值时 非齐次线性方程组 (1)有唯一解；(2)无解；(3)有无穷多解?请帮忙给出正确答案和分析
λ取何值时，非齐次线性方程组 (1)有唯一解；(2)无解；(3)有无穷多解?请帮忙给出正确答案和分析，谢谢！
