如图1—19所示 两两相距为a的三个质点A B C 从t=0时刻开始分别以相同的速率v0运动 运动过
如图1—19所示，两两相距为a的三个质点A，B，C，从t=0时刻开始分别以相同的速率v0运动，运动过程中A的速度始终指着当时B所在的位置，B的速度始终指着当时C所在的位置，C的速度始终指着当时A所在的位置，试问三质点何时相遇。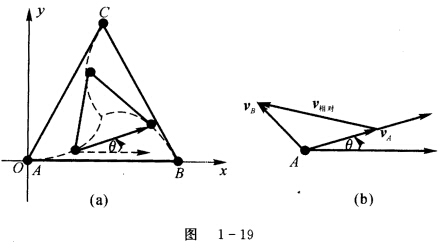 
请帮忙给出正确答案和分析，谢谢！
参考解答
456***101
2024-11-11 14:38:25
正确答案：由对称性知三质点ABC在任意时刻t仍然构成等边三角形设边长为l经极短时间△t后变为l+△l由余弦定理得 (l+△l)2=(v0△t)2+(l一v0△t)2一2(v0△t)(l一v0△t)cos60°简化为2l(△l)+(△l)2=3(v0△t)2一3l(v0△t)略去高阶小量得△l=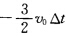
即边长缩短速率为
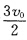从初始边长a缩短到零用时为
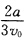。因此三质点ABC将在
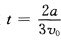时刻一起相遇。
由对称性知,三质点A,B,C在任意时刻t仍然构成等边三角形,设边长为l,经极短时间△t后变为l+△l,由余弦定理得(l+△l)2=(v0△t)2+(l一v0△t)2一2(v0△t)(l一v0△t)cos60°简化为2l(△l)+(△l)2=3(v0△t)2一3l(v0△t),略去高阶小量得△l=,即边长缩短速率为,从初始边长a缩短到零用时为。因此,三质点A,B,C将在时刻一起相遇。
相似问题
设方阵A满足A2一A一2E=O 证明A及A+2E都可逆 并求它们的逆矩阵请帮忙给出正确答案和分析 谢
设方阵A满足A2一A一2E=O，证明A及A+2E都可逆，并求它们的逆矩阵请帮忙给出正确答案和分析，谢谢！
已知3阶矩阵A可逆 将A的第2列与第3列交换得B 再把B的第1列的一2倍加到第3列得C 则满足PA-
已知3阶矩阵A可逆，将A的第2列与第3列交换得B，再把B的第1列的一2倍加到第3列得C，则满足PA-1=C-1的矩阵P为_____ A． B． C． D． 请帮忙给出正确答案和分析，谢谢！
设非负矩阵A∈Rn×n 若A有正特征向量x 则对所有m=1 2 …和i=1 2 … n 有 其中
设非负矩阵A∈Rn×n，若A有正特征向量x，则对所有m=1，2，…和i=1，2，…，n，有 ，其中Am=(ij(m))．特别地，若γ(A)>0，则对m=1，2，…，都有γ(A)－
设A为列满秩矩阵 AB=C 证明线性方程Bx=0与Cx=0同解．请帮忙给出正确答案和分析 谢谢！
设A为列满秩矩阵，AB=C，证明线性方程Bx=0与Cx=0同解．请帮忙给出正确答案和分析，谢谢！
设四元线性方程组(Ⅰ)为又已知齐次线性方程组(Ⅱ)的通解为k1(0 1 1 0)T+k2(一1 2
设四元线性方程组(Ⅰ)为又已知齐次线性方程组(Ⅱ)的通解为k1(0，1，1，0)T+k2(一1，2，2，1)T． (1)求方程组(Ⅰ)的基础解系． (2)问线性方程组(Ⅰ)和(
