实数域上二阶方阵所组成的线性空间V=M2(R)中 求它的一组基与维数．请帮忙给出正确答案和分析 谢谢

正确答案：对于V中一般元素α=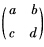我们希望找到一组结构最简单的元素线性表示α可考虑如下一组向量(V中的元素)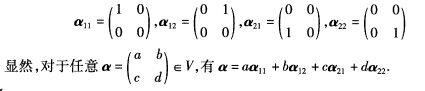： 即α可由α₁₁α₁₂α₂₁α₂₂线性表示． 下面再证明α₁₁α₁₂α₂₁α₂₂线性无关．由定义设k₁α₁₁+k₂α₁₂+k₃α₂₁+k₄α₂₂=0．则有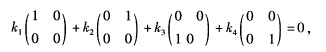即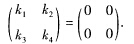所以有k₁=k₂=k₃=k₄=0故α₁₁α₁₂α₂₁α₂₂线性无关这样α₁₁α₁₂α₂₁α₂₂就构成V=M₂(R)的一组基而且V的维数为4．
对于V中一般元素α=我们希望找到一组结构最简单的元素线性表示α,可考虑如下一组向量(V中的元素)：即α可由α11,α12,α21,α22线性表示．下面再证明α11,α12,α21,α22线性无关．由定义,设k1α11+k2α12+k3α21+k4α22=0．则有即所以有k1=k2=k3=k4=0,故α11,α12,α21,α22线性无关,这样α11,α12,α21,α22就构成V=M2(R)的一组基,而且V的维数为4．