已知三阶实对称矩阵A的3个特征值为λ1=2 λ2 λ3=1且对应λ2 λ3的特征向量为 (1)求A
已知三阶实对称矩阵A的3个特征值为λ1=2，λ2，λ3=1且对应λ2，λ3的特征向量为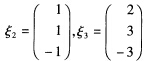 
(1)求A的与λ1=2对应的特征向量． (2)求矩阵A．
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***101
2024-11-11 03:57:51
正确答案：(1)设A的属于λ1=2的特征向量为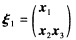
因为实对称矩阵的不同特征值对应的特征向量相互正交所以有(ξ1ξ2)=0(ξ1ξ3)=0即
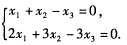由此解得A的属于λ1=2的特征向量为
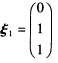(2)令 P=(ξ1ξ2ξ3)=
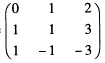则有 P-1AP=
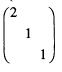从而得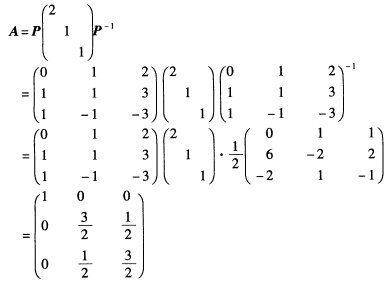
(1)设A的属于λ1=2的特征向量为因为实对称矩阵的不同特征值对应的特征向量相互正交,所以有(ξ1,ξ2)=0,(ξ1,ξ3)=0,即由此解得A的属于λ1=2的特征向量为(2)令P=(ξ1,ξ2,ξ3)=则有P-1AP=从而得
相似问题
求下列齐次线性方程组的基础解系： (3)nx1+(n一1)x2+…+2xn-1+xn=0．请帮忙给
求下列齐次线性方程组的基础解系： (3)nx1+(n一1)x2+…+2xn-1+xn=0．请帮忙给出正确答案和分析，谢谢！
写出下列二次型的矩阵： 请帮忙给出正确答案和分析 谢谢！
写出下列二次型的矩阵： 请帮忙给出正确答案和分析，谢谢！
已知线性齐次方程的基础解系为y1=ex y2=xex 则该方程为________．-请帮忙给出正确答
已知线性齐次方程的基础解系为y1=ex，y2=xex，则该方程为________．-请帮忙给出正确答案和分析，谢谢！
点(0 0)是函数z=x2-4xy+5y2-1的极________值点．请帮忙给出正确答案和分析 谢
点(0，0)是函数z=x2-4xy+5y2-1的极________值点．请帮忙给出正确答案和分析，谢谢！
设物体A从点(0 1)出发 以速度大小为常数v沿y轴正向运动．物体B从点(-1 0)与A同时出发 其
设物体A从点(0，1)出发，以速度大小为常数v沿y轴正向运动．物体B从点(-1，0)与A同时出发，其速度大小为2v，方向指向A求物体B的运动微分方程及初始条件．
