求下列齐次线性方程组的基础解系： (3)nx1+(n一1)x2+…+2xn-1+xn=0．请帮忙给
求下列齐次线性方程组的基础解系：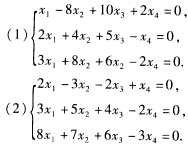 
(3)nx1+(n一1)x2+…+2xn-1+xn=0．
请帮忙给出正确答案和分析，谢谢！
参考解答
413***101
2024-11-11 03:53:02
正确答案：(1)对系数矩阵作初等行变换变为行最简形矩阵有
即得一个基础解系：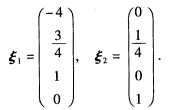
(2)施以初等行变换化简系数矩阵A为行最简形矩阵：
(3)系数矩阵为(nn一1…21)因系数矩阵的秩为1未知量的个数为n因此基础解系应含有n一1个解向量取x1x2…xn-1为自由未知量今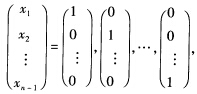
则对应有xn=一n一(n+1)…一2即得基础解系(表示为一个矩阵)：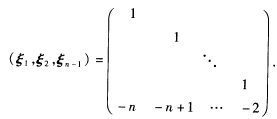
(1)对系数矩阵作初等行变换,变为行最简形矩阵,有即得一个基础解系：(2)施以初等行变换化简系数矩阵A为行最简形矩阵：(3)系数矩阵为(n,n一1,…,2,1),因系数矩阵的秩为1,未知量的个数为n,因此基础解系应含有n一1个解向量,取x1,x2,…,xn-1为自由未知量,今则对应有xn=一n,一(n+1),…,一2,即得基础解系(表示为一个矩阵)：
相似问题
写出下列二次型的矩阵： 请帮忙给出正确答案和分析 谢谢！
写出下列二次型的矩阵： 请帮忙给出正确答案和分析，谢谢！
已知线性齐次方程的基础解系为y1=ex y2=xex 则该方程为________．-请帮忙给出正确答
已知线性齐次方程的基础解系为y1=ex，y2=xex，则该方程为________．-请帮忙给出正确答案和分析，谢谢！
点(0 0)是函数z=x2-4xy+5y2-1的极________值点．请帮忙给出正确答案和分析 谢
点(0，0)是函数z=x2-4xy+5y2-1的极________值点．请帮忙给出正确答案和分析，谢谢！
设物体A从点(0 1)出发 以速度大小为常数v沿y轴正向运动．物体B从点(-1 0)与A同时出发 其
设物体A从点(0，1)出发，以速度大小为常数v沿y轴正向运动．物体B从点(-1，0)与A同时出发，其速度大小为2v，方向指向A求物体B的运动微分方程及初始条件．
线性微分方程的解具有什么样的结构特征?请帮忙给出正确答案和分析 谢谢！
线性微分方程的解具有什么样的结构特征?请帮忙给出正确答案和分析，谢谢！
