判别下列二阶曲线的类型： (1)2χ12＋χ22＋3χ32－4χ1χ3＋6χ2χ3－4χ1χ3＝0；
判别下列二阶曲线的类型： (1)2χ12＋χ22＋3χ32－4χ1χ3＋6χ2χ3－4χ1χ3＝0； (2)4χ12＋15χ22－5χ32＋16χ1χ2－22χ2χ3－8χ1χ3＝0．
请帮忙给出正确答案和分析，谢谢！
参考解答
463***102
2024-11-19 10:28:58
正确答案：(1)由于｜aij｜＝
＝－4≠0 又因为它上面有实点(12＋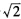
0)所以二阶曲线为非退化实二阶曲线． (2)由于｜aij｜＝0且(aj)的秩为2又因为它上面有实点(－1
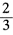0)所以二阶曲线为退化二阶曲线是一对实相交直线．
(1)由于｜aij｜＝＝－4≠0又因为它上面有实点(1,2＋,0),所以二阶曲线为非退化实二阶曲线．(2)由于｜aij｜＝0且(aj)的秩为2,又因为它上面有实点(－1,,0),所以二阶曲线为退化二阶曲线,是一对实相交直线．
相似问题
下面所说的名称或定理 哪些属于射影几何学?哪些属于仿射几何学?哪些属于欧氏几何学(最大的)? (1)
下面所说的名称或定理，哪些属于射影几何学?哪些属于仿射几何学?哪些属于欧氏几何学(最大的)? (1)梯形；(2)正方形；(3)离心率； (4)塞瓦定理与麦尼劳斯
设B′C′ C′A′ A′B′分别是A(a1 a2 a3) B(b1 b2 b3) C(c1 c2
设B′C′，C′A′，A′B′分别是A(a1，a2，a3)、B(b1，b2，b3)、C(c1，c2，c3)关于S=0的极线，求证三点形ABC与A′B′C′透视．请帮忙给出正确答案和分析，谢谢！
试用二次曲线的射影定义 求出满足下列条件的二次曲线方程． (1)通过五点(1 0 －1) (1 0
试用二次曲线的射影定义，求出满足下列条件的二次曲线方程． (1)通过五点(1，0，－1)，(1，0，1)，(1，2，1)，(1，2，－1)，(1，3，0)； (2)通过五点(1
设p1≡a1χ＋b1y＋c1 p2≡a2χ＋b2y＋c2 p3≡a3χ＋b3y＋c3 证明：以p1＝
设p1≡a1χ＋b1y＋c1，p2≡a2χ＋b2y＋c2，p3≡a3χ＋b3y＋c3，证明：以p1＝0，p2＝0，p3＝0为边的三角形的重心坐标由以下方程给出： (a2b3－a3b2)p1＝(
若(P1P2 P3P4)＝4 则(P1P2 P4P3)＝_______ (P1P3 P2P4)＝__
若(P1P2，P3P4)＝4，则(P1P2，P4P3)＝_______，(P1P3，P2P4)＝_______，(P2P3，P4P1)＝_______．请帮忙给出正确答案和分析，谢谢！
