设p1≡a1χ＋b1y＋c1 p2≡a2χ＋b2y＋c2 p3≡a3χ＋b3y＋c3 证明：以p1＝

正确答案：如图2—3—25三角形ABC的边BC、CA、AB的方程分别为P₁＝0、P₂＝0、P₃＝0G为／X ABC的垂心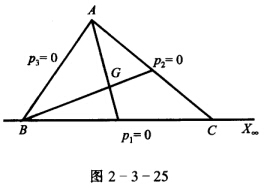． 设X_∞为P₁上的无穷远点则直线AX_∞的方程可以写为P₂＋2λp₃＝0即 a₂χ₁＋b₂χ₂＋c₂χ₃＋λ(a₃χ₁＋b₃χ₂＋c₃χ₃)＝0 因X_∞为(b₁－a₁0) 故有：a₂b₁－b₂a₁＋λ(a₃b₁－b₃a₁)＝0． 所以λ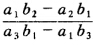＝． 由于G是垂心所以AB、AC与AG、AX_∞调和共轭所以AG的方程是P₂－λ2p₃＝0． 将λ值代入上式得AG的方程为： (a₃b₁－a₁b₃)P₂＝(a₁b₂－a₂b₁)P₃． 同理可以求出BG、CG的方程分别为： (a₂b₃－a₃b₂)P₁＝(a₁b₂－a₂b₁)P₃ (a₂b₃－a₃b₂)P₁＝(a₃b₁－a₁b₃)P₂ 所以命题得证．
如图2—3—25,三角形ABC的边BC、CA、AB的方程分别为P1＝0、P2＝0、P3＝0,G为／XABC的垂心．设X∞为P1上的无穷远点,则直线AX∞的方程可以写为P2＋2λp3＝0,即a2χ1＋b2χ2＋c2χ3＋λ(a3χ1＋b3χ2＋c3χ3)＝0因X∞为(b1,－a1,0),故有：a2b1－b2a1＋λ(a3b1－b3a1)＝0．所以λ＝．由于G是垂心,所以AB、AC与AG、AX∞调和共轭,所以AG的方程是P2－λ2p3＝0．将λ值代入上式,得AG的方程为：(a3b1－a1b3)P2＝(a1b2－a2b1)P3．同理可以求出BG、CG的方程分别为：(a2b3－a3b2)P1＝(a1b2－a2b1)P3,(a2b3－a3b2)P1＝(a3b1－a1b3)P2,所以命题得证．