设B′C′ C′A′ A′B′分别是A(a1 a2 a3) B(b1 b2 b3) C(c1 c2
设B′C′，C′A′，A′B′分别是A(a1，a2，a3)、B(b1，b2，b3)、C(c1，c2，c3)关于S=0的极线，求证三点形ABC与A′B′C′透视．
请帮忙给出正确答案和分析，谢谢！
参考解答
490***102
2024-11-19 10:20:19
正确答案：如图1—5一14因为C′A′是B(b1b2b3)关于S＝0的极线所以C′A′的方程为Sb＝0 ①．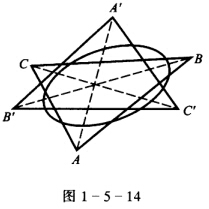
同理A′B′的方程为Sc＝0②所以AA′的方程为Sb＋2Sc＝0③又A′A通过A点所以Sab＋λSac＝0由此得：λ＝
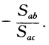． 代人③得到A′A的方程为： SacSb－SabSc＝0 ④ 同理B′B的方程为： SabSc－SbcSa＝0 ⑤ C′C的方程为： SbcSa－ScaSb＝0 ⑥ ④＋⑤＋⑥得： (SacSb－SabSc)＋(SabSc－SbcSa)＋(SbcSa－ScaSb)＝0 所以AA′BB′CC′三线共点．即三点形ABC和AB′C′透视．
如图1—5一14,因为C′A′是B(b1,b2,b3)关于S＝0的极线,所以C′A′的方程为Sb＝0①．同理A′B′的方程为Sc＝0②,所以AA′的方程为Sb＋2Sc＝0③,又A′A通过A点,所以Sab＋λSac＝0,由此得：λ＝．代人③得到A′A的方程为：SacSb－SabSc＝0,④同理,B′B的方程为：SabSc－SbcSa＝0,⑤C′C的方程为：SbcSa－ScaSb＝0,⑥④＋⑤＋⑥得：(SacSb－SabSc)＋(SabSc－SbcSa)＋(SbcSa－ScaSb)＝0所以AA′,BB′,CC′三线共点．即三点形ABC和A,B′C′透视．
相似问题
试用二次曲线的射影定义 求出满足下列条件的二次曲线方程． (1)通过五点(1 0 －1) (1 0
试用二次曲线的射影定义，求出满足下列条件的二次曲线方程． (1)通过五点(1，0，－1)，(1，0，1)，(1，2，1)，(1，2，－1)，(1，3，0)； (2)通过五点(1
设p1≡a1χ＋b1y＋c1 p2≡a2χ＋b2y＋c2 p3≡a3χ＋b3y＋c3 证明：以p1＝
设p1≡a1χ＋b1y＋c1，p2≡a2χ＋b2y＋c2，p3≡a3χ＋b3y＋c3，证明：以p1＝0，p2＝0，p3＝0为边的三角形的重心坐标由以下方程给出： (a2b3－a3b2)p1＝(
若(P1P2 P3P4)＝4 则(P1P2 P4P3)＝_______ (P1P3 P2P4)＝__
若(P1P2，P3P4)＝4，则(P1P2，P4P3)＝_______，(P1P3，P2P4)＝_______，(P2P3，P4P1)＝_______．请帮忙给出正确答案和分析，谢谢！
设四直线[1 0 1] [0 1 1] [1 1 1] [0 0 1]分别对应四直线[1 0 0]
设四直线[1，0，1]，[0，1，1]，[1，1，1]，[0，0，1]分别对应四直线[1，0，0]，[0，l，0]，[0，0，1]，[1，1，1]，求射影对应式．请帮忙给出正确答案和分析，谢谢！
设直线上射影坐标系的基点为A1 A2 E 如果A1是直线上的无穷点 求线段AE2中点的射影左边．请帮
设直线上射影坐标系的基点为A1，A2，E，如果A1是直线上的无穷点，求线段AE2中点的射影左边．请帮忙给出正确答案和分析，谢谢！
