证明：曲面M：x(u v)=(3u(1+v2)一u3 3v(1+u2)一v3 3(u2一v2))是极

正确答案：(1)计算得x_u^'=(3(1+v²一u²)6uv6u)x_v^'=(6uv3(1+u²一v²)一6v)所以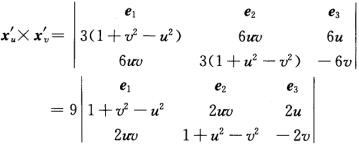=9(2u(一2v²一1一u²+v²)2v(1+v²一u²+2u²)1一(v²一u²)²一4u²v²)=9(一2u(1+u²+v²)2v(1+u²+v²)1一(u²+v²)²)=9(一2u(1+u²+v²)2v(1+u²+v²)(1一u²一v²)(1+u²+v²))=9(1+u²+v²)(一2u2v1一u²一v²)．单位法向量为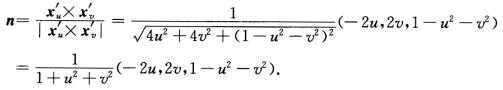于是E=x_u^'.x_u^'=9[(1+v²一u²)²+4u²v²+4u²=9(1+u²+v²)²F=x_u^'.x_v^'=0G=x_v^'.x_v^'=9[4u²v²+(1+u²一v²)²+4v²=9(1+u²+v²)²I=Edu²+2Fdudv+Gdv²=9(1+u²+v²)²(du²+dv²)．x_uu^''=(一6u6v6)x_vv^''=(6u一6v一6)x_uv^''=(6v6u0)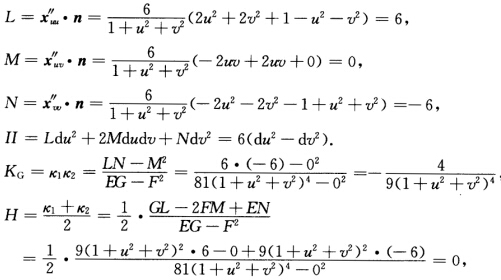故M为极小曲面．主曲率k₁k₂满足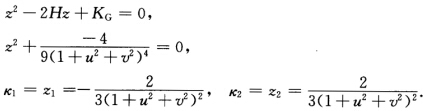：或者由F=M=0及定理2．5．6知两参数曲线为正交曲率线网．另一方面正因为F=0即参数曲线正交故根据定理2．5．6的证明有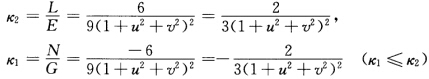于是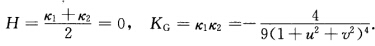根据定理2．5．5曲率线v=v₀所在的平面为y一v₀z=[3v₀(1+u²)一v₀³一v₀.3(u²一v₀)=3v₀+2v₀³．曲率线u=u₀所在的平面为x+u₀z=[3u₀(1+v²)一u₀³+u₀.3(u₀²一v²)=3u₀+2u₀³．
(1)计算得xu'=(3(1+v2一u2),6uv,6u),xv'=(6uv,3(1+u2一v2),一6v),所以=9(2u(一2v2一1一u2+v2),2v(1+v2一u2+2u2),1一(v2一u2)2一4u2v2)=9(一2u(1+u2+v2),2v(1+u2+v2),1一(u2+v2)2)=9(一2u(1+u2+v2),2v(1+u2+v2),(1一u2一v2)(1+u2+v2))=9(1+u2+v2)(一2u,2v,1一u2一v2)．单位法向量为于是E=xu'.xu'=9[(1+v2一u2)2+4u2v2+4u2=9(1+u2+v2)2,F=xu'.xv'=0,G=xv'.xv'=9[4u2v2+(1+u2一v2)2+4v2=9(1+u2+v2)2,I=Edu2+2Fdudv+Gdv2=9(1+u2+v2)2(du2+dv2)．xuu''=(一6u,6v,6),xvv''=(6u,一6v,一6),xuv''=(6v,6u,0),故M为极小曲面．主曲率k1,k2满足：或者由F=M=0及定理2．5．6知,两参数曲线为正交曲率线网．另一方面,正因为F=0,即参数曲线正交,故根据定理2．5．6的证明,有于是根据定理2．5．5,曲率线v=v0所在的平面为y一v0z=[3v0(1+u2)一v03一v0.3(u2一v0)=3v0+2v03．曲率线u=u0所在的平面为x+u0z=[3u0(1+v2)一u03+u0.3(u02一v2)=3u0+2u03．