已知射影坐标变换式：设直线上从第一个射影坐标系到第二个射影坐标系的变换将三点的坐标(1 0) (1
已知射影坐标变换式：设直线上从第一个射影坐标系到第二个射影坐标系的变换将三点的坐标(1，0)，(1，
设直线上从第一个射影坐标系到第二个射影坐标系的变换将三点的坐标(1，0)，(1，1)，(2，1)分别变为(1，0)，(－1，3)，(1，4)，求这个坐标变换公式．
请帮忙给出正确答案和分析，谢谢！
参考解答
432***102
2024-11-19 23:34:34
正确答案：坐标变换公式为：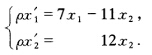
坐标变换公式为：
相似问题
试证非对合的射影变换一定可分解成两个对合之积 并将如下射影变换φ分解成两个对合之积： 试证：成试证：
试证非对合的射影变换一定可分解成两个对合之积，并将如下射影变换φ分解成两个对合之积： 试证：成试证：成对合对应的二线束中，一般只有一对对应直线
下列哪些图形具有射影性质? (1)平行直线； (2)三点共线； (3)三直线共点； (4)两点间的距
下列哪些图形具有射影性质? (1)平行直线； (2)三点共线； (3)三直线共点； (4)两点间的距离； (5)两直线的夹角； (6)两相等线段．请帮忙给出正确答案和分析，谢谢！
已知共线点(AA′ BC)＝(BB′ CA)＝(CC′ AB)＝－1 求证：(AA′ B′C′)＝(
已知共线点(AA′，BC)＝(BB′，CA)＝(CC′，AB)＝－1，求证：(AA′，B′C′)＝(BB′，C，A′)＝－1．请帮忙给出正确答案和分析，谢谢！
设点列的底是l P P′；Q Q′是l上的射影变换的两对对应点 E是自对应点 V V′是通过E的直线
设点列的底是l，P、P′；Q、Q′是l上的射影变换的两对对应点，E是自对应点，V，V′是通过E的直线上的任意两点，PV与P′V′交于P〞，QV与Q′V′交于Q〞，
求下列对合的自对应点的坐标：已知射影坐标变换： ρχ′1＝－χ1＋χ2＋χ3 ρχ′2＝χ1－χ2
求下列对合的自对应点的坐标：已知射影坐标变换： ρχ′1＝－χ1＋χ2＋χ3， ρχ′2＝χ1－χ2＋χ3， 已知射影坐标变换： ρχ′1＝－χ1＋χ2＋
