已知共线点(AA′ BC)＝(BB′ CA)＝(CC′ AB)＝－1 求证：(AA′ B′C′)＝(
已知共线点(AA′，BC)＝(BB′，CA)＝(CC′，AB)＝－1，求证：(AA′，B′C′)＝(BB′，C，A′)＝－1．
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***102
2024-11-19 23:18:18
正确答案：以A(a)A′(a′)为基点设BB′的坐标顺次为：a＋λa′a＋λ′a′． 因为 (AA′BC)＝－1所以C的坐标为a－2a′． 又(BB′CA)＝－1． 故有(λ＋λ)(λ′－0)＝－(λ－0)(λ′＋λ)． 解得λ′＝－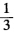
λ所以B′的坐标为a－
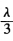a′． 同理可得C′的坐标为a＋
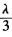a′． 所以(AA′B′C′)
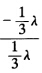＝－1． 将
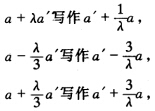故有(BB′C′A′)＝
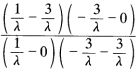＝－1．
以A(a),A′(a′)为基点,设B,B′的坐标顺次为：a＋λa′,a＋λ′a′．因为(AA′,BC)＝－1,所以C的坐标为a－2a′．又(BB′,CA)＝－1．故有(λ＋λ)(λ′－0)＝－(λ－0)(λ′＋λ)．解得λ′＝－λ,所以B′的坐标为a－a′．同理可得C′的坐标为a＋a′．所以(AA′,B′C′)＝－1．将,故有(BB′,C′A′)＝＝－1．
相似问题
设点列的底是l P P′；Q Q′是l上的射影变换的两对对应点 E是自对应点 V V′是通过E的直线
设点列的底是l，P、P′；Q、Q′是l上的射影变换的两对对应点，E是自对应点，V，V′是通过E的直线上的任意两点，PV与P′V′交于P〞，QV与Q′V′交于Q〞，
求下列对合的自对应点的坐标：已知射影坐标变换： ρχ′1＝－χ1＋χ2＋χ3 ρχ′2＝χ1－χ2
求下列对合的自对应点的坐标：已知射影坐标变换： ρχ′1＝－χ1＋χ2＋χ3， ρχ′2＝χ1－χ2＋χ3， 已知射影坐标变换： ρχ′1＝－χ1＋χ2＋
问：射影直线上的一点能将射影直线剖分成两部分吗?射影平面上的一直线能将射影平面剖分成两部分吗?请帮忙
问：射影直线上的一点能将射影直线剖分成两部分吗?射影平面上的一直线能将射影平面剖分成两部分吗?请帮忙给出正确答案和分析，谢谢！
已知射影坐标变换式：求射影对应的坐标表示式 使直线l上坐标是1 2 3的三点对应l′上的三点 其坐标
已知射影坐标变换式：求射影对应的坐标表示式，使直线l上坐标是1，2，3的三点对应l′上的三点，其坐标求射影对应的坐标表示式，使直线l上坐标是1，2，3的
求下列对合的自对应点的坐标：求使三点(0 0) (1 0) (0 1)分别对应(0 0) (0 1)
求下列对合的自对应点的坐标：求使三点(0，0)，(1，0)，(0，1)分别对应(0，0)，(0，1)，(1，0)且使直线χ＋y＋1求使三点(0，0)，(1，0)，(0，1)分别对应(
