设m n是正整数 则反常积分的收敛性A.仅与m值有关.B.仅与n值有关.C.与m n值都有关.D.与
设m,n是正整数,则反常积分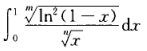 的收敛性
的收敛性
A.仅与m值有关.
B.仅与n值有关.
C.与m,n值都有关.
D.与m,n值都无关.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:D
[分析x=0、1为瑕点,插入分点,利用比较判别法判断两个无界函数反常积分的敛散性.[详解。对I1,因为,且对任意正整数m,n,有,由比较判别法的极限形式知,无论正整数m,n取何值,反常积分I1是收敛的.对I2,由比较判别法知无论正整数m,n取何值反常积分I2是收敛的,因此应选(D).[评注根据考试大纲的要求,此题属超纲范围.
相似问题
设f(x) g(x)在[a b]上连续 且满足 ∫axf(t)dt≥∫axg(t)dt x∈[a b
设f(x),g(x)在[a,b]上连续,且满足 ∫axf(t)dt≥∫axg(t)dt,x∈[a,b),∫abf(t)dt=∫abg(t)dt. 证明:∫abxf(x)dx≤∫abxg(x)dx.请帮忙给出正确答案和分析,谢谢!
如图1—3—17 一容器的内侧是由图中曲线绕y轴旋转一周而成的曲面 该曲线由x2+y2=2y与x2+
如图1—3—17,一容器的内侧是由图中曲线绕y轴旋转一周而成的曲面,该曲线由x2+y2=2y与x2+y2=1连接而成的. (1)求容器的体积; (2)若将容器内盛满
已知抛物线y=px2+qx(其中p<0 q>0)在第一象限内与直线x+y=5相切 且此抛物线与x轴所
已知抛物线y=px2+qx(其中p<0,q>0)在第一象限内与直线x+y=5相切,且此抛物线与x轴所围成的平面图形的面积为S. (1)问p和q为何值时,S达到最大值?
当物体的温度高于周围介质的湿度时 物体就不断冷却.若物体的温度T与时间t的函数关系为T=T(t).应
当物体的温度高于周围介质的湿度时,物体就不断冷却.若物体的温度T与时间t的函数关系为T=T(t).应怎样确定该物体在时刻t的冷却速度?请帮忙给出正确答案
设f(x)在[a b]上连续 在(a b)内可导(0<a<b) 证明:在(a b)内至少有一点c 使
设f(x)在[a,b]上连续,在(a,b)内可导(0<a<b),证明:在(a,b)内至少有一点c,使得2c[f(b)-f(a)]=fˊ(c)(b2-a2).请帮忙给出正确答案和分析,谢谢!












