如图1—3—17 一容器的内侧是由图中曲线绕y轴旋转一周而成的曲面 该曲线由x2＋y2＝2y与x2＋
如图1—3—17，一容器的内侧是由图中曲线绕y轴旋转一周而成的曲面，该曲线由x2＋y2＝2y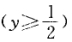
与x2＋y2＝1
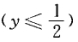连接而成的． (1)求容器的体积； (2)若将容器内盛满的水从容器顶部全部抽出，至少需要做多少功?(长度单位：m，重力加速度为gm／s2，水的密度为103kg／m3)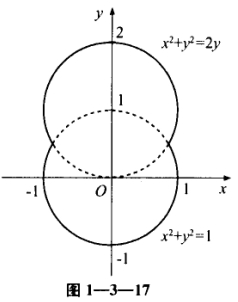 
请帮忙给出正确答案和分析，谢谢！
参考解答
473***101
2024-11-09 15:59:56
正确答案：(1)旋转体分为体积相等的两部分于是 容器的体积为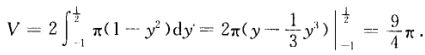 
或者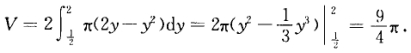
(2)利用微元法所做功的计算也分为两部分：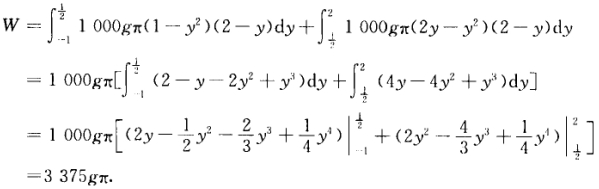
利用旋转体的体积公式计算容器的体积，利用微元法求所做的功．
相似问题
已知抛物线y＝px2＋qx(其中p＜0 q＞0)在第一象限内与直线x＋y＝5相切 且此抛物线与x轴所
已知抛物线y＝px2＋qx(其中p＜0，q＞0)在第一象限内与直线x＋y＝5相切，且此抛物线与x轴所围成的平面图形的面积为S． (1)问p和q为何值时，S达到最大值?
当物体的温度高于周围介质的湿度时 物体就不断冷却．若物体的温度T与时间t的函数关系为T＝T(t)．应
当物体的温度高于周围介质的湿度时，物体就不断冷却．若物体的温度T与时间t的函数关系为T＝T(t)．应怎样确定该物体在时刻t的冷却速度?请帮忙给出正确答案
设f(x)在[a b]上连续 在(a b)内可导(0＜a＜b) 证明：在(a b)内至少有一点c 使
设f(x)在[a，b]上连续，在(a，b)内可导(0＜a＜b)，证明：在(a，b)内至少有一点c，使得2c[f(b)－f(a)]＝fˊ(c)(b2－a2)．请帮忙给出正确答案和分析，谢谢！
设直线y＝ax与抛物线．y＝x2所围成图形的面积为S1 它们与直线x＝1所围成图形的面积为S2 并且
设直线y＝ax与抛物线．y＝x2所围成图形的面积为S1，它们与直线x＝1所围成图形的面积为S2，并且a＜1． (1)试确定a的值，使S1＋S2达到最小，并求出最小值
假设曲线l1：y＝1－x2(0≤x≤1)与x轴和y轴所围成区域被曲线l2：y＝ax2分为面积相等的两
假设曲线l1：y＝1－x2(0≤x≤1)与x轴和y轴所围成区域被曲线l2：y＝ax2分为面积相等的两：部分，其中a是大于零的常数，试确定a的值．请帮忙给出正确答案和
