若A=(αij)∈Cn×n不可约 且存在i0使得 则有r(A)
若A=(αij)∈Cn×n不可约，且存在i0使得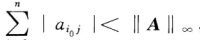
，则有r(A)<∥A∥∞．
请帮忙给出正确答案和分析，谢谢！
参考解答
432***101
2024-11-11 23:11:21
正确答案：因为γ(A)≤∥A∥∞所以只需证明γ(A)≠∥A∥∞即可．对于任意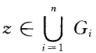
存在i1使∣z－αi1i1∣≤Ri1由三角不等式可得
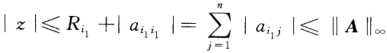即
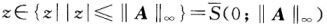因此并集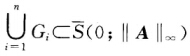
假设在定理条件下γ(A)=∥A∥∞则A至少有一个特征值λ0满足∣λ0∣=γ(A)=∥A∥∞所以λ0在
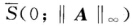的边界上．从而λ0亦在A的n个盖尔圆并集的边界上．由定理14知∣λ0－αij∣=Ri i=12…n．特别地有∣λ0－αi0i0∣=Ri0于是
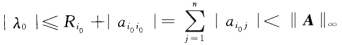这与假设矛盾故应有γ(A)≠∥A∥∞．
因为γ(A)≤∥A∥∞,所以只需证明γ(A)≠∥A∥∞即可．对于任意,存在i1使∣z－αi1i1∣≤Ri1,由三角不等式可得,即因此并集假设在定理条件下,γ(A)=∥A∥∞,则A至少有一个特征值λ0满足∣λ0∣=γ(A)=∥A∥∞,所以λ0在的边界上．从而λ0亦在A的n个盖尔圆并集的边界上．由定理14知∣λ0－αij∣=Ri,i=1,2,…,n．特别地有∣λ0－αi0i0∣=Ri0于是这与假设矛盾,故应有γ(A)≠∥A∥∞．
相似问题
若A是正规矩阵 证明：(1)A+A=AA+；(2)(An)+=(A+)n．请帮忙给出正确答案和分析
若A是正规矩阵，证明：(1)A+A=AA+；(2)(An)+=(A+)n．请帮忙给出正确答案和分析，谢谢！
设∥x∥a ∥x∥b是Cn上的两个向量范数 a1 a2是两个正实数 证明： (1)max{∥x∥a
设∥x∥a，∥x∥b是Cn上的两个向量范数，a1，a2是两个正实数，证明： (1)max{∥x∥a，∥x∥b}=∥x∥c； (2)a1∥x∥a+a2∥x∥b=∥x∥d；都是Cn上的向量
设A B∈Cn×n 当．AB=BA时 计算可知eAeB=eBeA=eA+B． (1)试举例说明 一般
设A，B∈Cn×n，当．AB=BA时，计算可知eAeB=eBeA=eA+B． (1)试举例说明，一般情况下eAeB=eBeA=eA+B可能不成立； (2)证明∣eA∣ ∣eB∣=∣eB∣ ∣eA∣=
设A(k)∈Cm×n B(k)∈Cn×l 证明请帮忙给出正确答案和分析 谢谢！
设A(k)∈Cm×n，B(k)∈Cn×l，，证明请帮忙给出正确答案和分析，谢谢！
验证下列方程组是不相容的 并用A+求它的最佳逼近解． 请帮忙给出正确答案和分析 谢谢！
验证下列方程组是不相容的，并用A+求它的最佳逼近解． 请帮忙给出正确答案和分析，谢谢！
