证明：圆上任一点与圆内接正方形各顶点的连线组成一调和线束．请帮忙给出正确答案和分析 谢谢！
证明：圆上任一点与圆内接正方形各顶点的连线组成一调和线束．
请帮忙给出正确答案和分析，谢谢！
参考解答
420***102
2024-11-19 14:29:37
正确答案：如图1—3—6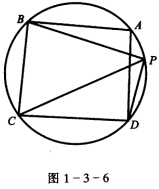
因为∠APB＝∠BPC＝∠CPD＝
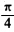故PBPD是∠APC的内外角平分线． 所以P(ACBD)＝－1．
如图1—3—6因为∠APB＝∠BPC＝∠CPD＝故PB,PD是∠APC的内外角平分线．所以P(AC,BD)＝－1．
相似问题
证明：一直线上的射影变换证明：任何一个群都与一个变换群同构．证明：任何一个群都与一个变换群同构．请帮
证明：一直线上的射影变换证明：任何一个群都与一个变换群同构．证明：任何一个群都与一个变换群同构．请帮忙给出正确答案和分析，谢谢！
为什么向量的数量积的概念在仿射几何里不存在?请帮忙给出正确答案和分析 谢谢！
为什么向量的数量积的概念在仿射几何里不存在?请帮忙给出正确答案和分析，谢谢！
设点(1 0 0) (1 1 1)分别对应点(－1 1 1) (1 1 1) 直线χ1＋χ2＋χ3＝
设点(1，0，0)，(1，1，1)分别对应点(－1，1，1)，(1，1，1)，直线χ1＋χ2＋χ3＝0，χ2＝0分别对应直线χ′3＝0，2χ′1＋2χ′3＝0，求射影对应式．请
设A B C是不同的共线三点 求A B C分别对应B C A所决定的射影变换的方程与自对应点．请帮忙
设A、B、C是不同的共线三点，求A、B、C分别对应B、C、A所决定的射影变换的方程与自对应点．请帮忙给出正确答案和分析，谢谢！
证明：由平面上四个射影变换： 试证：平面上的非奇线性变换：的集合G构成变换群．问这个群是不是可换试证
证明：由平面上四个射影变换： 试证：平面上的非奇线性变换：的集合G构成变换群．问这个群是不是可换试证：平面上的非奇线性变换：的集合G构成变换群．
