证明：由平面上四个射影变换： 试证：平面上的非奇线性变换：的集合G构成变换群．问这个群是不是可换试证
证明：由平面上四个射影变换： 试证：平面上的非奇线性变换：的集合G构成变换群．问这个群是不是可换
试证：平面上的非奇线性变换：
的集合G构成变换群．问这个群是不是可换群?
请帮忙给出正确答案和分析，谢谢！
参考解答
463***102
2024-11-19 14:05:36
正确答案：(1)任取φ1、φ2∈G．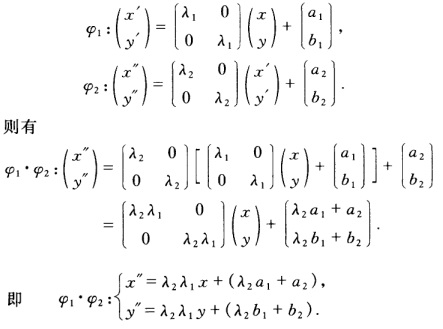
其中λ2λ1＞0λ2a1＋a2λb1＋b2都是实数所以φ.φ∈G． (2)设
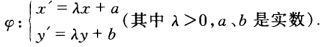则
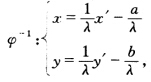其中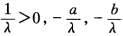
都是实数所以φ1-∈G． 根据(1)(2)可知G构成群． 不难验证：不是对任何φ1φ2∈G都有φ1.φ2＝φ2.φ1所以G不是可换群．
(1)任取φ1、φ2∈G．其中λ2λ1＞0,λ2a1＋a2,λb1＋b2都是实数,所以φ.φ∈G．(2)设则其中都是实数,所以φ1-∈G．根据(1)(2)可知G构成群．不难验证：不是对任何φ1,φ2∈G,都有φ1.φ2＝φ2.φ1,所以G不是可换群．
相似问题
给定配极变换： 求点(1 1 1)在直线[2 1 1]上的共轭点．请帮忙给出正确答案和分析 谢谢！
给定配极变换： 求点(1，1，1)在直线[2，1，1]上的共轭点．请帮忙给出正确答案和分析，谢谢！
恒等变换构成群 问对于这个群有没有相应的几何学?请帮忙给出正确答案和分析 谢谢！
恒等变换构成群，问对于这个群有没有相应的几何学?请帮忙给出正确答案和分析，谢谢！
设坐标三点形的顶点A1 A2 A3与单位点E的笛氏坐标分别为(1 1 1) (一1 1 1) (0
设坐标三点形的顶点A1，A2，A3与单位点E的笛氏坐标分别为(1，1，1)，(一1，1，1)，(0，0，1)，(0，1，2)，求在此射影坐标系里直线A3A1，A1A2，A2A1的方程
用代数法证明帕斯卡定理请帮忙给出正确答案和分析 谢谢！
用代数法证明帕斯卡定理请帮忙给出正确答案和分析，谢谢！
问下列每个集合关于所给的运算是否构成群? (1)G：全体实数 运算：普通乘法； (2)G：全体整数
问下列每个集合关于所给的运算是否构成群? (1)G：全体实数，运算：普通乘法； (2)G：全体整数，运算：普通乘法； (3)G：全体偶数，运算：普通加法；
