设∥.∥是Cm×n上的矩阵算子范数 若A∈Cm×n满足∥A∥
设∥.∥是Cm×n上的矩阵算子范数，若A∈Cm×n满足∥A∥<1，证明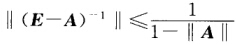
请帮忙给出正确答案和分析，谢谢！
参考解答
420***101
2024-11-11 23:33:08
正确答案：因为γ(A)≤∥A∥＜1故(E－A)－1存在．又因为 ．(E－A)－1(E－A)=E(E－A)－1=E+(E－A)－1 A．所以∥(E－A)－1∥≤∥E∥+∥(E－A)－1A∥.∥A∥=1+∥(E－A)－1A∥.∥A∥即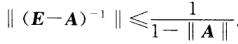
因为γ(A)≤∥A∥＜1,故(E－A)－1存在．又因为．(E－A)－1(E－A)=E,(E－A)－1=E+(E－A)－1A．所以∥(E－A)－1∥≤∥E∥+∥(E－A)－1A∥.∥A∥=1+∥(E－A)－1A∥.∥A∥,即
相似问题
试证明： (AHA)+=A+(AH)+ (AAH)+=(AH)+A+ (AHA)+=A+(AAH
试证明： (AHA)+=A+(AH)+， (AAH)+=(AH)+A+， (AHA)+=A+(AAH)+A=AH(AAH)+(AH)+，AA+=(AAH)(AAH)+=(AAH)+(AAH)．请帮忙给出正确答案和分析，谢谢！
求矩阵A=的谱分解式 并给出An的表达式．请帮忙给出正确答案和分析 谢谢！
求矩阵A=的谱分解式，并给出An的表达式．请帮忙给出正确答案和分析，谢谢！
已知A为一个四阶矩阵 其特征值为0 0 π －π 求sin A COS A eA．请帮忙给出正确答案
已知A为一个四阶矩阵，其特征值为0，0，π，－π，求sin A，COS A，eA．请帮忙给出正确答案和分析，谢谢！
若A=(αij)∈Cn×n奇异 则存在某个i0 使请帮忙给出正确答案和分析 谢谢！
若A=(αij)∈Cn×n奇异，则存在某个i0，使请帮忙给出正确答案和分析，谢谢！
若A=(αij)∈Cn×n不可约 且存在i0使得 则有r(A)
若A=(αij)∈Cn×n不可约，且存在i0使得，则有r(A)<∥A∥∞．请帮忙给出正确答案和分析，谢谢！
