求矩阵A=的谱分解式 并给出An的表达式．请帮忙给出正确答案和分析 谢谢！
求矩阵A=
的谱分解式，并给出An的表达式．
请帮忙给出正确答案和分析，谢谢！
参考解答
481***101
2024-11-11 23:18:08
正确答案：先求矩阵A的特征值．由det(λE－A)=(λ+2)(λ－7)2得矩阵A的特征值为λ1=－2λ23=7对应的特征向量分别为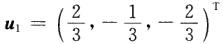
μ2=(－0.57580．79820．1767)Tμ3=(0．47320．5017－0．7241)T令U=(μ1μ2μ3)UH=
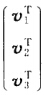A1=μ1v1TA2=μ2v2TA3=μ3v3T则A的谱分解为A=－2A1+7A2+7A3．所以An=(－2)nA1+7nA2+7nA3．
先求矩阵A的特征值．由det(λE－A)=(λ+2)(λ－7)2,得矩阵A的特征值为λ1=－2,λ2,3=7,对应的特征向量分别为,μ2=(－0.5758,0．7982,0．1767)T,μ3=(0．4732,0．5017,－0．7241)T,令U=(μ1μ2μ3)UH=,A1=μ1v1T,A2=μ2v2TA3=μ3v3T,则A的谱分解为A=－2A1+7A2+7A3．所以An=(－2)nA1+7nA2+7nA3．
相似问题
已知A为一个四阶矩阵 其特征值为0 0 π －π 求sin A COS A eA．请帮忙给出正确答案
已知A为一个四阶矩阵，其特征值为0，0，π，－π，求sin A，COS A，eA．请帮忙给出正确答案和分析，谢谢！
若A=(αij)∈Cn×n奇异 则存在某个i0 使请帮忙给出正确答案和分析 谢谢！
若A=(αij)∈Cn×n奇异，则存在某个i0，使请帮忙给出正确答案和分析，谢谢！
若A=(αij)∈Cn×n不可约 且存在i0使得 则有r(A)
若A=(αij)∈Cn×n不可约，且存在i0使得，则有r(A)<∥A∥∞．请帮忙给出正确答案和分析，谢谢！
若A是正规矩阵 证明：(1)A+A=AA+；(2)(An)+=(A+)n．请帮忙给出正确答案和分析
若A是正规矩阵，证明：(1)A+A=AA+；(2)(An)+=(A+)n．请帮忙给出正确答案和分析，谢谢！
设∥x∥a ∥x∥b是Cn上的两个向量范数 a1 a2是两个正实数 证明： (1)max{∥x∥a
设∥x∥a，∥x∥b是Cn上的两个向量范数，a1，a2是两个正实数，证明： (1)max{∥x∥a，∥x∥b}=∥x∥c； (2)a1∥x∥a+a2∥x∥b=∥x∥d；都是Cn上的向量
