已知下列矩阵A 试用各种方法求A+. 请帮忙给出正确答案和分析 谢谢!
已知下列矩阵A,试用各种方法求A+. 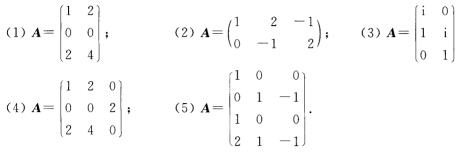
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)奇异值分解法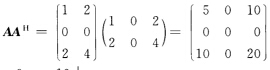 由
由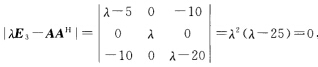 得AAH的特征值λ1=25λ2=0.而对应于λ1=25的单位特征向量为
得AAH的特征值λ1=25λ2=0.而对应于λ1=25的单位特征向量为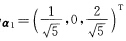 故U1=(α1).
故U1=(α1).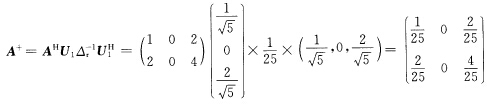 (2)最大秩分解法显然A是行满秩矩阵则
(2)最大秩分解法显然A是行满秩矩阵则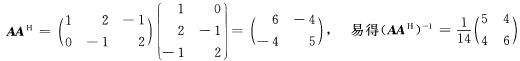 易得
易得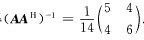 所以
所以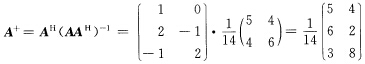 (3)极限算法
(3)极限算法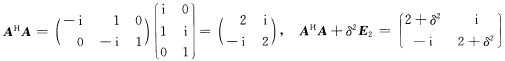 容易算得
容易算得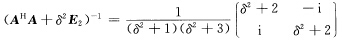 于是
于是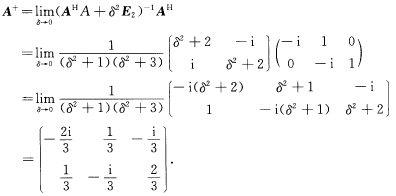 (4)谱分解法
(4)谱分解法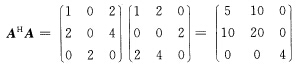
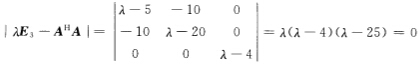 故AHA的特征值为λ1=4λ2=25λ3=0.于是
故AHA的特征值为λ1=4λ2=25λ3=0.于是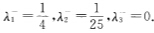 设P1(λ)-(λ-λ2)(λ-λ3)-λ(λ-25)P2(λ)-(λ-λ1)(λ-λ3)-λ(λ-4)P3(λ)-(λ-λ1)(λ-λ2)-(λ-4)(λ-25).可求得P1(λ1)=4(4-25)=-84P2(A2)=25(25-4)=525P1(AHA)-(AHA-25E3)AHAP2(AHA)-(AHA-4E3)AHA.于是
设P1(λ)-(λ-λ2)(λ-λ3)-λ(λ-25)P2(λ)-(λ-λ1)(λ-λ3)-λ(λ-4)P3(λ)-(λ-λ1)(λ-λ2)-(λ-4)(λ-25).可求得P1(λ1)=4(4-25)=-84P2(A2)=25(25-4)=525P1(AHA)-(AHA-25E3)AHAP2(AHA)-(AHA-4E3)AHA.于是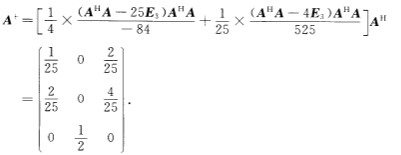 (5)最大秩分解法容易得到A的一个满秩分解表达式
(5)最大秩分解法容易得到A的一个满秩分解表达式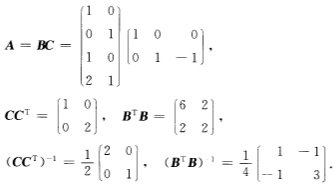 于是
于是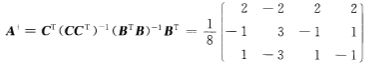
(1)奇异值分解法由,得AAH的特征值λ1=25,λ2=0.而对应于λ1=25的单位特征向量为,故U1=(α1).(2)最大秩分解法显然A是行满秩矩阵,则,易得所以(3)极限算法容易算得于是(4)谱分解法故AHA的特征值为λ1=4,λ2=25,λ3=0.于是设P1(λ)-(λ-λ2)(λ-λ3)-λ(λ-25),P2(λ)-(λ-λ1)(λ-λ3)-λ(λ-4),P3(λ)-(λ-λ1)(λ-λ2)-(λ-4)(λ-25).可求得P1(λ1)=4(4-25)=-84,P2(A2)=25(25-4)=525,P1(AHA)-(AHA-25E3)AHA,P2(AHA)-(AHA-4E3)AHA.于是(5)最大秩分解法容易得到A的一个满秩分解表达式于是
相似问题
设∥.∥是Cm×n上的矩阵算子范数 若A∈Cm×n满足∥A∥
设∥ ∥是Cm×n上的矩阵算子范数,若A∈Cm×n满足∥A∥<1,证明请帮忙给出正确答案和分析,谢谢!
试证明: (AHA)+=A+(AH)+ (AAH)+=(AH)+A+ (AHA)+=A+(AAH
试证明: (AHA)+=A+(AH)+, (AAH)+=(AH)+A+, (AHA)+=A+(AAH)+A=AH(AAH)+(AH)+,AA+=(AAH)(AAH)+=(AAH)+(AAH).请帮忙给出正确答案和分析,谢谢!
求矩阵A=的谱分解式 并给出An的表达式.请帮忙给出正确答案和分析 谢谢!
求矩阵A=的谱分解式,并给出An的表达式.请帮忙给出正确答案和分析,谢谢!
已知A为一个四阶矩阵 其特征值为0 0 π -π 求sin A COS A eA.请帮忙给出正确答案
已知A为一个四阶矩阵,其特征值为0,0,π,-π,求sin A,COS A,eA.请帮忙给出正确答案和分析,谢谢!
若A=(αij)∈Cn×n奇异 则存在某个i0 使请帮忙给出正确答案和分析 谢谢!
若A=(αij)∈Cn×n奇异,则存在某个i0,使请帮忙给出正确答案和分析,谢谢!












