如图1—27所示 一质量为M 长为L的带形挡板 静止放在水平地面上 设板与地动摩擦因数与静摩擦因数皆
如图1—27所示,一质量为M、长为L的带形挡板,静止放在水平地面上,设板与地动摩擦因数与静摩擦因数皆为μ。质量为m的人从板的一端由静止开始相对于地面匀加速地向前走向另一端,到达另一端时便骤然停止在板上。已知人与板的静摩擦因数足够大,人在板上不滑动。试求板滑动的最大距离。 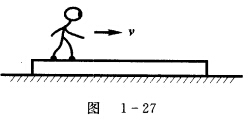
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:只要设法使人和板系统获得尽量大的向前动量即可。人在板上走动设板向后运动以t表示人从板的一端由静止开始走向另一端所用时间。设板向后运动x1以f表示人与板的摩擦力以F表示板与地的摩擦力a1和a2表示人与板的加速度则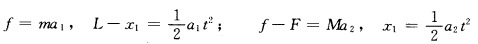 解得
解得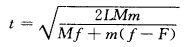 人和板系统所受外力为F人骤然停止人和板有共同速度为v忽略碰撞所用时间由冲量定理有 Ft=(M+m)v 设人和板一块移动的距离为x2由动能定理有
人和板系统所受外力为F人骤然停止人和板有共同速度为v忽略碰撞所用时间由冲量定理有 Ft=(M+m)v 设人和板一块移动的距离为x2由动能定理有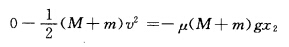 板净移动的距离为
板净移动的距离为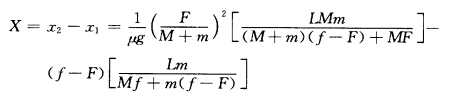 要使X最大有f=Ff=Fmax=μ(M+m)g故
要使X最大有f=Ff=Fmax=μ(M+m)g故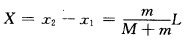
只要设法使人和板系统获得尽量大的向前动量即可。人在板上走动,设板向后运动,以t表示人从板的一端由静止开始走向另一端所用时间。设板向后运动x1,以f表示人与板的摩擦力,以F表示板与地的摩擦力,a1和a2表示人与板的加速度,则解得人和板系统所受外力为F,人骤然停止,人和板有共同速度为v,忽略碰撞所用时间,由冲量定理有Ft=(M+m)v设人和板一块移动的距离为x2,由动能定理有板净移动的距离为要使X最大,有f=F,f=Fmax=μ(M+m)g,故
相似问题
有关船舶租用合同的请求权 自知道或者应当知道权利被侵害之日起计算 时效期间为( )A 一年B 二年C
有关船舶租用合同的请求权,自知道或者应当知道权利被侵害之日起计算,时效期间为( )A、一年B、二年C、三年D、六年
设A B都是m×n矩阵 证明A≌B的充分必要条件是R(A)=R(B).请帮忙给出正确答案和分析 谢谢
设A、B都是m×n矩阵,证明A≌B的充分必要条件是R(A)=R(B).请帮忙给出正确答案和分析,谢谢!
求下列方程组的通解 请帮忙给出正确答案和分析 谢谢!
求下列方程组的通解 请帮忙给出正确答案和分析,谢谢!
依据提单收货人抬头的记载不同 提单可以分为( )A 清洁提单B 收货待运提单C 不记名提单D 记名提
依据提单收货人抬头的记载不同,提单可以分为( )A、清洁提单B、收货待运提单C、不记名提单D、记名提单E、指示提单
设A∈Rn×n ∥A∥是Rn×n上的任意一种矩阵范数 则请帮忙给出正确答案和分析 谢谢!
设A∈Rn×n,∥A∥是Rn×n上的任意一种矩阵范数,则请帮忙给出正确答案和分析,谢谢!












