将下列函数按勒让德多项式展开： (1)f(x)=x3 (2)f(x)=|x| 请帮忙给出正确答案和分
将下列函数按勒让德多项式展开： (1)f(x)=x3 (2)f(x)=|x| 
请帮忙给出正确答案和分析，谢谢！
参考解答
413***102
2024-11-18 01:57:45
正确答案：(1)由于f(x)的最高次幂是3所以展开式为 f(x) =C0P0(x)+C1P1(x)+C2P2(x)+C3P3(x)将Pn(x)的多项式代入有 x3=C0P0(x)+C1P1(x)+C2P2(x)+C3P3(x)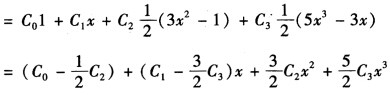
比较x的同次幂的系数可得
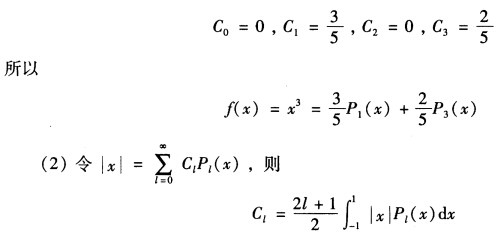因为|x|是偶函数故当Pι(x)为奇函数即当n=2n+1n=012…时 Cι=C2n+1=0于是
(1)由于f(x)的最高次幂是3,所以展开式为f(x)=C0P0(x)+C1P1(x)+C2P2(x)+C3P3(x)将Pn(x)的多项式代入,有x3=C0P0(x)+C1P1(x)+C2P2(x)+C3P3(x)比较x的同次幂的系数,可得因为|x|是偶函数,故当Pι(x)为奇函数,即当n=2n+1,n=0,1,2,…时Cι=C2n+1=0于是
相似问题
证明：(1)两个奇函数之和为奇函数 其积为偶函数； (2)两个偶函数之和与积都为偶函数； (3)奇函
证明：(1)两个奇函数之和为奇函数，其积为偶函数； (2)两个偶函数之和与积都为偶函数； (3)奇函数与偶函数之积为奇函数。请帮忙给出正确答案和分析，谢谢！
设0≤α≤1。求证：f(x)=xα在区间[0 +∞)上一致连续。请帮忙给出正确答案和分析 谢谢！
设0≤α≤1。求证：f(x)=xα在区间[0，+∞)上一致连续。请帮忙给出正确答案和分析，谢谢！
设f(x)为[-α α]上的奇(偶)函数。证明：若f(x)在[0 α]上增 则f(x)在[-α 0]
设f(x)为[-α，α]上的奇(偶)函数。证明：若f(x)在[0，α]上增，则f(x)在[-α，0]上增(减)。请帮忙给出正确答案和分析，谢谢！
设定义在R上的函数f(x)在0 1两点连续 且对任何x∈R有f(x2)=f(x)。证明：f(x)为常
设定义在R上的函数f(x)在0，1两点连续，且对任何x∈R有f(x2)=f(x)。证明：f(x)为常量函数。请帮忙给出正确答案和分析，谢谢！
若对任何充分小的ε＞0 f(x)在[α+ε b-ε]上连续 能否由此推出f(x)在(α b)上连续?
若对任何充分小的ε＞0，f(x)在[α+ε，b-ε]上连续，能否由此推出f(x)在(α，b)上连续?请帮忙给出正确答案和分析，谢谢！
