设曲面M的第3基本形式为Ⅲ=edu2＋2fdudv＋gdv2． 证明： (1)设曲面上无抛物点(即K
设曲面M的第3基本形式为Ⅲ=edu2＋2fdudv＋gdv2． 证明： (1)设曲面上无抛物点(即KG≠0处处成立)，则该
设曲面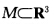
上无抛物点(即KG≠0处处成立)，则该曲面上的点与单位球面S2在Gauss映射G：M→S2下的像G(M)是局部一对一的(是否是整体一对一的?参阅定理3．3．4)．
请帮忙给出正确答案和分析，谢谢！
参考解答
406***102
2024-11-17 01:01:57
正确答案：因为KG≠0处处成立并从定理2．6．3(1)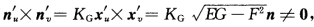
立知Gauss映射的Jacobi行列式不为0．根据逆映射定理(参阅[8第108页定理8．4．3)Gauss映射G是局部一对一的．
因为KG≠0处处成立,并从定理2．6．3(1),立知Gauss映射的Jacobi行列式不为0．根据逆映射定理(参阅[8第108页定理8．4．3),Gauss映射G是局部一对一的．
相似问题
求曲面F(x y z)=0的测地线x(s)=(x(s) y(s) z(s)) 其中s为其弧长请帮忙给
求曲面F(x，y，z)=0的测地线x(s)=(x(s)，y(s)，z(s))，其中s为其弧长请帮忙给出正确答案和分析，谢谢！
用E F G及其偏导函数表达Fijk．请帮忙给出正确答案和分析 谢谢！
用E，F，G及其偏导函数表达Fijk．请帮忙给出正确答案和分析，谢谢！
证明：曲面M：x(u v)=(3u(1+v2)一u3 3v(1+u2)一v3 3(u2一v2))是极
证明：曲面M：x(u，v)=(3u(1+v2)一u3，3v(1+u2)一v3，3(u2一v2))是极小曲面(Enneper曲面)，其曲率线是平面曲线，并求出曲率线所在的平面．请帮忙给出正确答案和分析，谢谢！
证明：(1)(2)其中g=det(gij)．请帮忙给出正确答案和分析 谢谢！
证明：(1)(2)其中g=det(gij)．请帮忙给出正确答案和分析，谢谢！
求悬链面M：求双曲抛物面M：x(u v)=(a(u＋v) b(u一v)2uv) (a>0 b>0)(
求悬链面M：求双曲抛物面M：x(u,v)=(a(u＋v),b(u一v)2uv) (a>0，b>0)(它的直角坐标方程为的渐求双曲抛物面M：x(u,v)=(a(u+v),b(u一v)2uv) (a>0，b>0)(
