设X～N(0 1) Y～N(0 1) 且ρXY=0 问X与Y是否独立?请帮忙给出正确答案和分析 谢谢

正确答案：如果(XY)服从二维正态分布则结论是肯定的：X与Y一定独立．如果没有“(XY)服从二维正态分布”的条件X与Y有可能不独立．见下面的例子． 令g(xy)=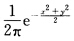则显然g(xy)为连续函数而且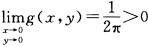．不妨取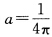由g(xy)的连续性存在l＞0使当｜x｜≤l｜y｜≤l时g(xy)≥a．令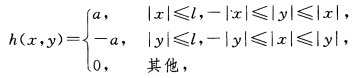则h(xy)满足 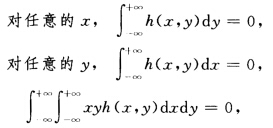令 f(xy)=g(xy)+h(xy)则由g(xy)和h(xy)的构造及上述特性．可见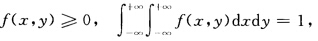因而是一个二维随机变量的概率密度．设(XY)的概率密度为f(xy)．则关于X和关于Y的边缘概率密度分别为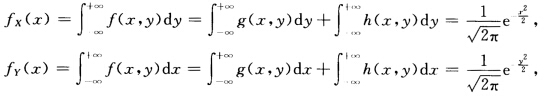即X～N(01)Y～N(01)．因而E(X)=E(Y)=0D(X)=D(Y)=1．而且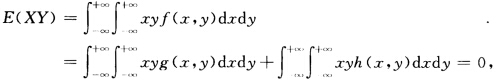因而Cov(XY)=0ρ_XY=0．然而显然有 f(xy)≠f_X(x)_Y(y)｜x｜≤Z｜y｜≤l可见X与Y不独立．
此题很容易使人给出错误的回答：X与Y独立．这个答案之所以错误就在于忽略了下面关于正态随机变量的一个结论中的条件：“若(X，Y)服从二维正态分布”．这个结论是：若(X，Y)服从二维正态分布，则X与Y独立的充分必要条件是X与Y不相关．因而要说明本例中的X与y可以不独立，只需举一这样的例子．(X，Y)不服从二维正态分布且不相互独立，但关于X和关于y的边缘分布是一维正态分布，又ρXY=0.这个例子可以这样做：先令g(x，y)=，再做一个二元函数h(x，y)，使得对任意x，有∫—∞+∞h(x，y)dy=0．对任意y，有∫—∞+∞h(x，y)dy=0．又∫—∞+∞∫—∞+∞xyh(x，y)dxdy=0，而且f(x，y)=g(x，y)+h(x，y)≥0，这样可以保证f(x，y)为二维概率密度．边缘分布都是N(0，1)，而且f(x，y)对应的协方差为零．