设L是一条平面曲线 其上任意一点P(x y)(x＞0)到坐标原点的距离恒等于该点处的切线在y轴上的截
设L是一条平面曲线，其上任意一点P(x，y)(x＞0)到坐标原点的距离恒等于该点处的切线在y轴上的截距，且L经过点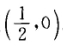
． (1)试求曲线L的方程； (2)求L位于第一象限部分的一条切线，使该切线与L以及两坐标轴所围图形的面积最小．
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***101
2024-11-09 11:47:43
正确答案：(1)设曲线L上过点P(xy)的切线方程为Y—y＝y'(X－x)令X＝0得该切线在y轴上的截距为y－xy'．由题设有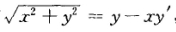
此为一阶齐次微分方程令
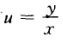将此方程转化为
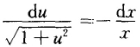两边积分并代入
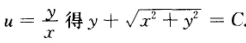。由于L经过点
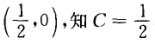于是L的方程为
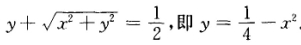。(2)设第一象限内曲线
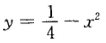在点P(xy)处的切线方程为
它与x轴及y轴的交点分别为
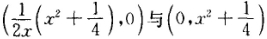。于是所求面积为
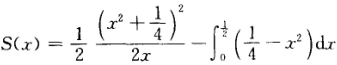令 S'(x)＝0得
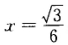容易验证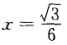
是函数S(x)在
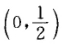内的极小值点且是唯一的极小值点即为最小值点．于是所求切线为
。
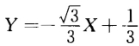[分析(1)先求出切线方程及其在y轴上的截距，由题设可得到与待求曲线对应的函数所满足的微分方程．(2)由面积最小，可得曲线上的切点，从而求出对应的切线方程．[评注本题是一道综合题，主要考查由实际问题建立微分方程的能力、微分方程的求解、导数与定积分的几何应用以及求函数的极值．求曲线在任意点P(x，y)处的切线方程时，由于任意点已用x和y表示，因此切线上任意点的坐标设为(X，Y)，以示区别．这是求解这类问题的一种习惯做法，应引起注意．
相似问题
设f(x)为连续函数 请帮忙给出正确答案和分析 谢谢！
设f(x)为连续函数，请帮忙给出正确答案和分析，谢谢！
设y＝y(x)是区间(－π π)内过点的光滑曲线．当－π＜x＜0时 曲线上任一点处的法线都过原点；当
设y＝y(x)是区间(－π，π)内过点的光滑曲线．当－π＜x＜0时，曲线上任一点处的法线都过原点；当0≤x＜π时，函数y(x)满足y"＋y＋x＝0． 求函数y(x)的
已知∫xf(x)dx＝arcsinx＋C 则＝_______．请帮忙给出正确答案和分析 谢谢！
已知∫xf(x)dx＝arcsinx＋C，则＝_______．请帮忙给出正确答案和分析，谢谢！
微分方程y'＋y＝x2＋1＋sinx的特解形式可设为A．y*＝ax2＋bx＋c＋x(Asinx＋Bc
微分方程y"＋y＝x2＋1＋sinx的特解形式可设为A．y*＝ax2＋bx＋c＋x(Asinx＋Bcosc)．B．y*＝x(ax2＋bx＋c＋Asinx＋Bcosx)．C．y*＝ax2＋bx＋c＋Asinx．D．
求下列图形的面积： (1)y＝x2－x＋2与通过坐标原点的两条切线所围成的图形； (2)y2＝2x与
求下列图形的面积： (1)y＝x2－x＋2与通过坐标原点的两条切线所围成的图形； (2)y2＝2x与点(1／2，1)处的法线所围成的图形．请帮忙给出正确答案和分析，谢谢！
