设y=y(x)是区间(-π π)内过点的光滑曲线.当-π<x<0时 曲线上任一点处的法线都过原点;当
设y=y(x)是区间(-π,π)内过点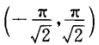 的光滑曲线.当-π<x<0时,曲线上任一点处的法线都过原点;当0≤x<π时,函数y(x)满足y"+y+x=0. 求函数y(x)的表达式.
的光滑曲线.当-π<x<0时,曲线上任一点处的法线都过原点;当0≤x<π时,函数y(x)满足y"+y+x=0. 求函数y(x)的表达式.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:当-π<x<0时设(xy)为曲线上任意一点由导数几何意义法线斜率为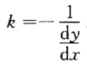 .由题意知法线斜率又为
.由题意知法线斜率又为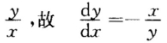 即 ydy=-xdx 两边积分得 y2=-x2+C. 由初始条件
即 ydy=-xdx 两边积分得 y2=-x2+C. 由初始条件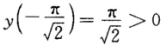 得C=π2
得C=π2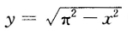 (-π<x<0) 当0≤x<π时有y'+y+x=0. 首先易得y'+y=0的通解为y*=C1cosx+C2sinx其次令y'+y+x=0的特解为y1=Ax+B则有0+Ax+B+x=0得A=-1B=0y1=-x因而y'+y+x=0的通解为y=C1cosx+C2sinx-x.由于y=y(x)是(-ππ)内的光滑曲线故y(x)在x=0处连续而且可导.于是
(-π<x<0) 当0≤x<π时有y'+y+x=0. 首先易得y'+y=0的通解为y*=C1cosx+C2sinx其次令y'+y+x=0的特解为y1=Ax+B则有0+Ax+B+x=0得A=-1B=0y1=-x因而y'+y+x=0的通解为y=C1cosx+C2sinx-x.由于y=y(x)是(-ππ)内的光滑曲线故y(x)在x=0处连续而且可导.于是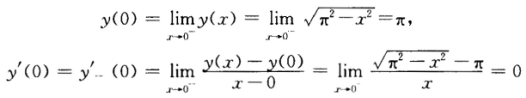 将上述条件代入y'+y+x=0的通解可得C1=πC2=1故 y=πcosx+sinx-x(0≤x<π). 所以y=y(x)的表达式为
将上述条件代入y'+y+x=0的通解可得C1=πC2=1故 y=πcosx+sinx-x(0≤x<π). 所以y=y(x)的表达式为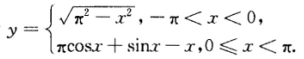 。
。
[分析本题考查导数的几何意义、微分方程求解和函数连续性,是一个比较综合的问题.在区间(-π,0)内,根据已知条件建立微分方程求解,在区间[0,π)上求解二阶常系数非齐次线性微分方程,并且根据曲线光滑条件确定任意常数.[评注1在区间[a,b上的光滑曲线y=f(x)指的是函数f(x)在区间[a,b上有一阶连续导数.[评注2在区间(-π,0)内的微分方程也可如下得到:曲线上任意一点(x,y)的法线方程为,又法线都过原点,即X=0,Y=0,代入即得微分方程yy'=-x.
相似问题
已知∫xf(x)dx=arcsinx+C 则=_______.请帮忙给出正确答案和分析 谢谢!
已知∫xf(x)dx=arcsinx+C,则=_______.请帮忙给出正确答案和分析,谢谢!
微分方程y'+y=x2+1+sinx的特解形式可设为A.y*=ax2+bx+c+x(Asinx+Bc
微分方程y"+y=x2+1+sinx的特解形式可设为A.y*=ax2+bx+c+x(Asinx+Bcosc).B.y*=x(ax2+bx+c+Asinx+Bcosx).C.y*=ax2+bx+c+Asinx.D.
求下列图形的面积: (1)y=x2-x+2与通过坐标原点的两条切线所围成的图形; (2)y2=2x与
求下列图形的面积: (1)y=x2-x+2与通过坐标原点的两条切线所围成的图形; (2)y2=2x与点(1/2,1)处的法线所围成的图形.请帮忙给出正确答案和分析,谢谢!
计算下列各弧长: (1)曲线y=lnx相应于的一段弧; (2)半立方抛物线的一支:y=x1/2上x=
计算下列各弧长: (1)曲线y=lnx相应于的一段弧; (2)半立方抛物线的一支:y=x1/2上x=0到x=1的一段弧; (3)星形线x=cos3t,y=sin3t的全长; (4
有一立体 底面是长轴为2a 短轴为2b的椭圆 而垂直于长轴的截面都是等边三角形 求其体积.请帮忙给出
有一立体,底面是长轴为2a,短轴为2b的椭圆,而垂直于长轴的截面都是等边三角形,求其体积.请帮忙给出正确答案和分析,谢谢!












