设二维随机变量(X Y)的分布律为 P{X=n Y=m}= m=0 1 2 … n n=0 1 2
设二维随机变量(X，Y)的分布律为 P{X=n，Y=m}=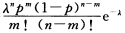
，m=0，1，2，…，n，n=0，1，2，…， 求关于X和关于Y的边缘分布律，问X与Y是否独立?
请帮忙给出正确答案和分析，谢谢！
参考解答
4j5***444
2023-11-13 18:35:16
正确答案：当n=012…取定
X～π(λp)． 由于当m＞n=012…时 P{X=nY=m)=0≠P{X=n)P{Y=m)＞0可见X与Y不独立．
利用，计算关于X和关于Y的边缘分布律，不过要注意的是：当m≤n时，才有，否则P{X=n，Y=m)=0．另外在求和时，用到二项公式及．
相似问题
设马尔可夫链有状态0 1 2 3和转移概率矩阵 试求f00(n)(n=1 2 3 4 5 …) 其
设马尔可夫链有状态0，1，2，3和转移概率矩阵 试求f00(n)(n=1，2，3，4，5，…)，其中fij(n)由P{Xn=i，Xk≠i，k=1，…，n一1｜X0=i}定义．请帮忙给出正确答案和分析，谢谢！
设随机变量X与Y独立同分布 且X的分布函数为F(x) 则Z=max{X Y}的分布函数为( )．A．
设随机变量X与Y独立同分布，且X的分布函数为F(x)，则Z=max{X，Y}的分布函数为( )．A．F2(x)B．F(x)F(y)C．1一[1一F(x)]2D．[1一F(x)][1一F(y)]请帮忙给出正确答案和分析，谢谢！
举一例说明：二维连续型随机变量(X Y)关于X Y的边缘分布都是正态分布 但X与Y的联合分布却不是正
举一例说明：二维连续型随机变量(X，Y)关于X，Y的边缘分布都是正态分布，但X与Y的联合分布却不是正态分布．请帮忙给出正确答案和分析，谢谢！
设随机变量(X Y)在区域D={(x y)：0≤x≤1 ｜y｜≤1)上服从均匀分布 求X与y的相关系
设随机变量(X，Y)在区域D={(x，y)：0≤x≤1，｜y｜≤1)上服从均匀分布，求X与y的相关系数及(X，Y)的协方差矩阵，问X与Y是否独立?是否不相关?请帮忙给出正
在成败型的重复试验中 每次试验结果为成功(S)或失败(F)．同一结果相继出现称为一个游程(run)
在成败型的重复试验中，每次试验结果为成功(S)或失败(F)．同一结果相继出现称为一个游程(run)，比如一串结果“FSSFFFS”中共有两个成功游程，三个失败游
