举一例说明：二维连续型随机变量(X Y)关于X Y的边缘分布都是正态分布 但X与Y的联合分布却不是正

正确答案：令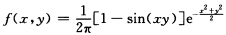． 首先由于1一sin(xy)≥0因此f(xy)≥0．又由于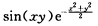关于x和y都是奇函数而且对取定的y积分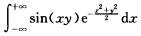收敛对取定的x积分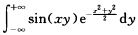收敛．因此有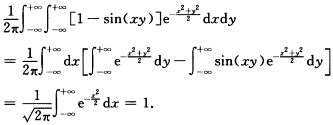可见f(xy)是一二概率密度． 由上面的计算容易得到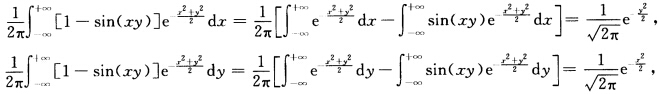即f(xy)关于X和关于Y的边缘分布都是N(01)分布但f(xy)显然不是二维正态概率密度．
不妨取边缘分布均为N(0，1)分布．为构造(X，Y)的概率密度f(x，y)，首先为使f(x，y)关于X和关于Y的边缘概率密度分别为，可以考虑将fx(x)fy(y)作为f(x，y)的一部分．其次，为使f(x，y)不是二维正态分布的概率密度，可考虑找一个二元函数g(x，y)，使得f(x，y)=fX(x)fY(y)一g(x，y)是一非正态的二元概率密度，且边缘概率密度仍是N(0，1)的概率密度，为此可以考虑g(x，y)=．这个函数关于x和关于y都是奇函数，而且对任意取定的x，积分收敛，因而积分为0，同理对任意取定的y，．另外由于｜sin(xy)｜≤1，因而1一sin(xy)≥0．于是f(x，y)=fX(x)fY(y)一g(x，y)=满足：f(x，y)≥0，且关于X和关于Y的边缘概率密度都是N(0，1)的概率密度，是一非正态分布的概率密度．