设二维随机变量(X1 X2)～N(1 1 22 22 ) Y1=X1+X2 Y2=X1一2X2 求(
设二维随机变量(X1，X2)～N(1，1，22，22，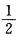
)，Y1=X1+X2，Y2=X1一2X2，求(Y1，Y2)的分布．
请帮忙给出正确答案和分析，谢谢！
参考解答
4j5***444
2023-11-13 22:24:40
正确答案：×
由题设知E(X1)一E(X2)=1,D(X1)=D(X2)=22,,因而Cov(X1,X2)=×2×2=2．记X=(X1,X2),μ=(1,1),C=．则X～N(μ,C)．记Y=(Y1,Y2),A=,YT=AXT．由正态随机变量的性质(3)知Y～N(μT,ACAT)．容易算得由此可见,E(Y1)=2,E(Y2)=一1,D(Y1)=D(Y2)=12,Cov(Y1,Y2)=一6,,于是有(Y1,Y2)～N(μ*,C*)或(Y1,Y2)～N(2,一1,12,12,一)．
相似问题
设离散型随机变量X服从超几何分布 其分布律为 P{X=k)= k=0 1 … l 其中N＞0 M＞
设离散型随机变量X服从超几何分布，其分布律为 P{X=k)=，k=0，1，…，l， 其中N＞0，M＞0，n≤N—M，l=min{M，n}．求E(X)和D(X)．请帮忙给出正确答案和分析，谢谢！
X(t)为一随机过程 a为常数 试以X(t)的自相关函数表出随机过程 y(t)=X(t+a)一X(t
X(t)为一随机过程，a为常数，试以X(t)的自相关函数表出随机过程 y(t)=X(t+a)一X(t) 的自相关函数．请帮忙给出正确答案和分析，谢谢！
设随机变量X与Y独立 且方差有限 证明： D(XY)=D(X)D(Y)+[E(X)]2D(y)+D(
设随机变量X与Y独立，且方差有限，证明： D(XY)=D(X)D(Y)+[E(X)]2D(y)+D(X)EE(Y)]2．请帮忙给出正确答案和分析，谢谢！
设(X Y)服从二维正态分布 且X～N(1 32) Y～N(0 42) ①求E(Z) D(Z)；
设(X，Y)服从二维正态分布，且X～N(1，32)，Y～N(0，42)，， ①求E(Z)，D(Z)； ②求ρXZ； ③问X与Z是否相互独立?为什么?请帮忙给出正确答案和分析，谢谢！
已知随机过程X(t)的均值μ(t)和协方差函数C(t1 t2) φ(t)是普通的函数 试求随机过程Y
已知随机过程X(t)的均值μ(t)和协方差函数C(t1，t2)，φ(t)是普通的函数，试求随机过程Y(t)=X(t)+φ(t)的均值和协方差函数．请帮忙给出正确答案和分析，谢谢！
