设A B C为三事件 试用A B C表示下列事件： (1)A B C至少有一个发生； (2)A B

正确答案：(1)由事件并的定义该事件可表示为A∪B∪C． (2)该事件可用两种方法表示．方法(I)直译(换句话说)该事件即是事件“A不发生而且B不发生而且C不发生”故可表为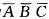；方法(Ⅱ)反译取余该事件的余是“A、B、C中至少有一个发生”A∪B∪C故它可表示为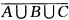．由事件的运算法则知两种表示法是一样的． (3)该事件可用三种方法表示．方法(I)直译该事件即是事件“ABC中至少有一个不发生”．故可表示为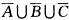；方法(Ⅱ)反译取余该事件的余是“ABC都发生”故它可表为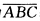；方法(Ⅲ)分解作并该事件可分解为下列3种情况：①“ABC中恰有一个不发生”可表示为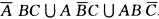．②“ABC中恰有两个不发生”可表示为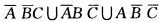．③“ABC都不发生”它可表示为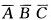而该事件是它们的并；因而(3)可表示为 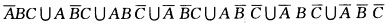．利用事件的运算法则可以证明上述3种表示法彼此相等． (4)该事件可用3种方法表示．方法(I)直译该事件即是事件“ABC中至少有2个不发生”．故可表示为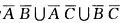；方法(Ⅱ)反译取余该事件的余是“ABC中至少有2个发生”AB∪AC∪BC故它可表示为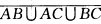；方法(Ⅲ)该事件可分解为下列2种情况：①“ABC中只有一个发生'可表示为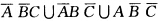．②“ABC都不发生”可表示为A B C而该事件是它们的并；因而(4)可表为 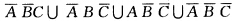利用事件的运算法则可以证明上述3种表示法彼此相等．
(1)由事件并的定义,该事件可表示为A∪B∪C．(2)该事件可用两种方法表示．方法(I)直译(换句话说),该事件即是事件“A不发生而且B不发生而且C不发生”,故可表为；方法(Ⅱ)反译取余,该事件的余是“A、B、C中至少有一个发生”,A∪B∪C,故它可表示为．由事件的运算法则知,两种表示法是一样的．(3)该事件可用三种方法表示．方法(I)直译,该事件即是事件“A,B,C中至少有一个不发生”．故可表示为；方法(Ⅱ)反译取余,该事件的余是“A,B,C都发生”,故它可表为；方法(Ⅲ)分解作并,该事件可分解为下列3种情况：①“A,B,C中恰有一个不发生”,可表示为．②“A,B,C中恰有两个不发生”,可表示为．③“A,B,C都不发生”,它可表示为,而该事件是它们的并；因而(3)可表示为．利用事件的运算法则,可以证明,上述3种表示法彼此相等．(4)该事件可用3种方法表示．方法(I)直译,该事件即是事件“A,B,C中至少有2个不发生”．故可表示为；方法(Ⅱ)反译取余,该事件的余是“A,B,C中至少有2个发生”,AB∪AC∪BC,故它可表示为；方法(Ⅲ)该事件可分解为下列2种情况：①“A,B,C中只有一个发生',可表示为．②“A,B,C都不发生”,可表示为ABC,而该事件是它们的并；因而(4)可表为利用事件的运算法则,可以证明,上述3种表示法彼此相等．