某公司有5个站点A1 A2 A3 A4 A5的货运任务 各任务的货运量a (单位：吨)如表4．33所
某公司有5个站点A1，A2，A3，A4，A5的货运任务，各任务的货运量a,(单位：吨)如表4．33所示。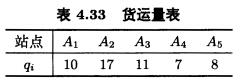
这些任务由配送中心O出发的载重量40吨和25吨的汽车来完成。中心O到各站点及各站点之间最短距离(单位：km)由表4．34给出。
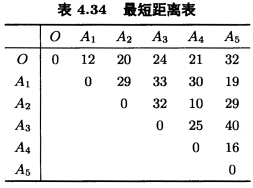试制定合理车辆行驶路线，以完成上述任务。
请帮忙给出正确答案和分析，谢谢！
参考解答
4j0***995
2024-10-30 10:16:03
正确答案：利用公式△dij{=Coi+Cjo—Cij得到表4．35、表4．36和表4．37。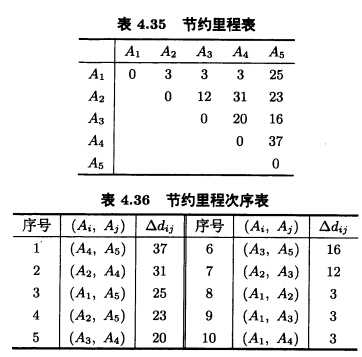
得配送路线：载重量40吨的汽车： O→A2→A4→A5→O总路程： 20+10+16+32=78(km)载重量25吨的汽车： O→A1→A3→O总路程： 12+33+24=69(km)总行驶里程： 78+69=147(km)
利用公式△dij{=Coi+Cjo—Cij得到表4．35、表4．36和表4．37。得配送路线：载重量40吨的汽车：O→A2→A4→A5→O总路程：20+10+16+32=78(km)载重量25吨的汽车：O→A1→A3→O总路程：12+33+24=69(km)总行驶里程：78+69=147(km)
相似问题
有A B C D四项任务分派给甲 乙 丙 丁四个人去做 这四个人都能承担上述四项任务 完成各项任务所
有A，B，C，D四项任务分派给甲、乙、丙、丁四个人去做，这四个人都能承担上述四项任务，完成各项任务所需时间如矩阵C1所示。问如何分派任务才能使完成任
考虑一量子数为n 在长度为l的一维势箱中运动的粒子。①求在势箱左端1/4区域找到粒子的概率；②n为何
考虑一量子数为n、在长度为l的一维势箱中运动的粒子。①求在势箱左端1 4区域找到粒子的概率；②n为何值时此概率最大?③n→∞时，此概率的极值为何值?说明
求下列交通图(图5．25一图5．27)所示场地设置问题的最优设场点。 (1) (2) (3)请帮忙给
求下列交通图(图5．25一图5．27)所示场地设置问题的最优设场点。 (1) (2) (3)请帮忙给出正确答案和分析，谢谢！
用图解法求下列线性规划的最优值：maxf=2x1+2x2且 请帮忙给出正确答案和分析 谢谢！
用图解法求下列线性规划的最优值：maxf=2x1+2x2且 请帮忙给出正确答案和分析，谢谢！
一个运输问题的运价 产量 销量由表4．38给出 用最小元素法写出初始调运方案表。 请帮忙给出正确答案
一个运输问题的运价、产量、销量由表4．38给出，用最小元素法写出初始调运方案表。 请帮忙给出正确答案和分析，谢谢！
