如图15—2所示 一段长为L的同轴电缆由内 外半径分别为R1 R2的导体圆筒构成 中间充有相对介电常
如图15—2所示,一段长为L的同轴电缆由内、外半径分别为R1、R2的导体圆筒构成,中间充有相对介电常量为εr的均匀各向同性的电介质.求: (1)当内筒带电量Q时,介质中的电位移、场强、极化强度和介质表面的束缚电荷; (2)介质中电场的储能. 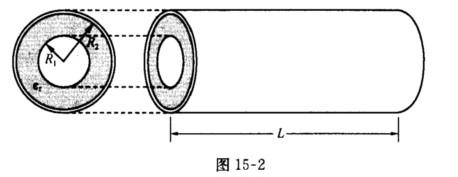
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:由导体静电平衡条件可知外筒内表面带电量为-Q设电缆单位长度带电为λ=Q/L. (1)忽略边缘效应介质中的电场沿径向且呈轴对称分布故取底面半径为r(R1<r<R2)、高为h(h<L)的同轴圆柱面为高斯面.由定义求出电位移通量为 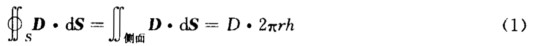 应用电介质中的高斯定理得到
应用电介质中的高斯定理得到  联立求解式(1)和式(2)得到
联立求解式(1)和式(2)得到 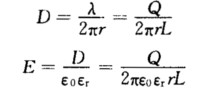 E的方向和D的方向均垂直于电缆轴线沿径向. 因D=ε0E+P有
E的方向和D的方向均垂直于电缆轴线沿径向. 因D=ε0E+P有 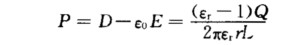 P的方向同E和D.由于介质是均匀的内外表面产生等量的束缚电荷故两个表面的面电荷密度不相等利用σ’=P.n并注意到内表面的法线方向指向轴线、外表面的法线方向背离轴线有
P的方向同E和D.由于介质是均匀的内外表面产生等量的束缚电荷故两个表面的面电荷密度不相等利用σ’=P.n并注意到内表面的法线方向指向轴线、外表面的法线方向背离轴线有 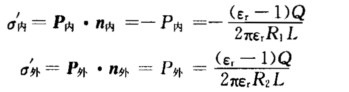 内、外表面的束缚电荷总量为
内、外表面的束缚电荷总量为 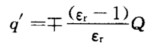 (2)电场的能量密度为
(2)电场的能量密度为 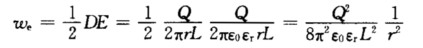 介质中储存的电场能量为
介质中储存的电场能量为 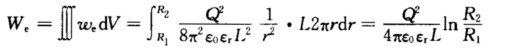 将这个表达式与电容器的储能公式(15-14)对比我们可以得到圆柱形电容器的电容公式(15-8).可见通过求解电场能量我们可以求得电容器的电容.这种方法在求解复杂体系的电容时极为有用.
将这个表达式与电容器的储能公式(15-14)对比我们可以得到圆柱形电容器的电容公式(15-8).可见通过求解电场能量我们可以求得电容器的电容.这种方法在求解复杂体系的电容时极为有用.
由导体静电平衡条件可知,外筒内表面带电量为-Q设电缆单位长度带电为λ=Q/L.(1)忽略边缘效应,介质中的电场沿径向且呈轴对称分布,故取底面半径为r(R1<r<R2)、高为h(h<L)的同轴圆柱面为高斯面.由定义求出电位移通量为应用电介质中的高斯定理,得到联立求解式(1)和式(2),得到E的方向和D的方向均垂直于电缆轴线沿径向.因D=ε0E+P,有P的方向同E和D.由于介质是均匀的,内外表面产生等量的束缚电荷,故两个表面的面电荷密度不相等,利用σ’=P.n,并注意到内表面的法线方向指向轴线、外表面的法线方向背离轴线,有内、外表面的束缚电荷总量为(2)电场的能量密度为介质中储存的电场能量为将这个表达式与电容器的储能公式(15-14)对比,我们可以得到圆柱形电容器的电容公式(15-8).可见,通过求解电场能量,我们可以求得电容器的电容.这种方法在求解复杂体系的电容时极为有用.
相似问题
在如图16-8所示电路中 电感线圈电阻r=25Ω 电抗XL=25Ω;电容器的容抗XC=50Ω R=5
在如图16-8所示电路中,电感线圈电阻r=25Ω,电抗XL=25Ω;电容器的容抗XC=50Ω,R=50Ω,如果电容支路的电流IC为2 5A,求:电源电压并用矢量图解法求总
举例论述下列说法是否正确?(1)电场强度相等的区域 电势处处相等;(2)电势相等处 电场强度也相等;
举例论述下列说法是否正确?(1)电场强度相等的区域,电势处处相等;(2)电势相等处,电场强度也相等;(3)电场强度大处,电势一定高;(4)电场强度
半径为R的均匀带电圆面 面电荷密度为σ。求其轴线上距圆心为x处的电场强度。请帮忙给出正确答案和分析
半径为R的均匀带电圆面,面电荷密度为σ。求其轴线上距圆心为x处的电场强度。请帮忙给出正确答案和分析,谢谢!
如图所示 一根载流I的导线 被折成长度分别为a b 夹角为120°的两段 并置于均匀磁场B中 若导
如图所示 一根载流I的导线,被折成长度分别为a、b,夹角为120°的两段,并置于均匀磁场B中,若导线的长度为b的一段与B平行,则a,b两段载流导线所受的
矩形截面的螺绕环 其尺寸如图17-7所示。已知线圈匝数为N。求通入电流I后 (1)环内外磁感应强度的
矩形截面的螺绕环,其尺寸如图17-7所示。已知线圈匝数为N。求通入电流I后,(1)环内外磁感应强度的分布;(2)通过螺绕环截面的磁通量。 请帮忙给出正












