设f(x)为不恒等于零的奇函数 Rf(0)存在 则函数g(x)=( ).A.在x=0处左极限不存在B
设f(x)为不恒等于零的奇函数,Rf(0)存在,则函数g(x)=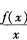 ( ).
( ).
A.在x=0处左极限不存在
B.有跳跃间断点x=0
C.在x=0处右极限不存在
D.有可去间断点x=0
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:D
由f(x)是奇函数有f(0)=0.又因为f'(0)存在,所以又因为x=0是g(x)的间断点,且,所以x=0是g(x)的可去间断点故应选D。
相似问题
设f(x) g(x)在[a b]上连续 (a b)内可导 证明存在ε∈(a b) 使得 [f(b)-
设f(x),g(x)在[a,b]上连续,(a,b)内可导,证明存在ε∈(a,b) 使得 [f(b)-f(a)]gˊ(ε)=[g(b)-g(a)]fˊ(ε)请帮忙给出正确答案和分析,谢谢!
用泰勒公式求下列极限: 试确定P的取值范围 使得y=x3-3x+p与x轴 (1)有一个交点;(2)有
用泰勒公式求下列极限: 试确定P的取值范围,使得y=x3-3x+p与x轴 (1)有一个交点;(2)有两个交点;(试确定P的取值范围,使得y=x3-3x+p与x轴 (1)有
设f(x)有一个原函数则请帮忙给出正确答案和分析 谢谢!
设f(x)有一个原函数则请帮忙给出正确答案和分析,谢谢!
利用函数奇偶性计算下列积分:设f(x)在(-∞ +∞)上有连续导数 且m≤f(x)≤M设f(x)在(
利用函数奇偶性计算下列积分:设f(x)在(-∞,+∞)上有连续导数,且m≤f(x)≤M设f(x)在(-∞,+∞)上有连续导数,且m≤f(x)≤M 请帮忙给出正确答案和分析,谢谢!
求y=|x|+|x—1|—|4—2x|的最大值与最小值.请帮忙给出正确答案和分析 谢谢!
求y=|x|+|x—1|—|4—2x|的最大值与最小值.请帮忙给出正确答案和分析,谢谢!












