可相似对角化，求x．参考解答
490***101
2024-11-11 07:26:41
正确答案：由A的特征多项式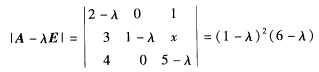
知A的特征值为λ=1(二重根)与λ=6．因A可对角化故A应有3个线性无关的特征向量单重特征值有λ=6对应着一个线性无关的特征向量那么二重特征值λ=1应对应两个线性无关的特征向量从而矩阵(A—E)的秩应为1．对(A—E)施以初等变换：
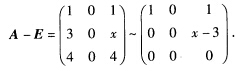由此可见当x=3时R(A—E)=1A的对应于特征值λ=1有两个线性无关的特征向量从而A有3个线性无关的特征向量即A可相似对角化．因此x=3为所求．
由A的特征多项式知,A的特征值为λ=1(二重根)与λ=6．因A可对角化,故A应有3个线性无关的特征向量,单重特征值有λ=6对应着一个线性无关的特征向量,那么二重特征值λ=1应对应两个线性无关的特征向量,从而矩阵(A—E)的秩应为1．对(A—E)施以初等变换：由此可见,当x=3时,R(A—E)=1,A的对应于特征值λ=1有两个线性无关的特征向量,从而A有3个线性无关的特征向量,即A可相似对角化．因此,x=3为所求．
相似问题
求一个正交变换化下列二次型成标准形： (1)f=2x12+3x22+3x32+4x2x3； (2)f
求一个正交变换化下列二次型成标准形： (1)f=2x12+3x22+3x32+4x2x3； (2)f=x12+x32+2x1x2—2x2x3．请帮忙给出正确答案和分析，谢谢！
某水库的水闸是下底为2 m 上底为6 m 高为10 m的梯形 则当水灌满时水闸所受的静压力为多少?请
某水库的水闸是下底为2 m，上底为6 m，高为10 m的梯形，则当水灌满时水闸所受的静压力为多少?请帮忙给出正确答案和分析，谢谢！
在R3中取两个基α1=(1 2 1)T α2=(2 3 3)T α3=(3 7 —2)T和β1=(3
在R3中取两个基α1=(1 2 1)T，α2=(2 3 3)T，α3=(3 7 —2)T和β1=(3 1 4)T，β2=(5 2 1)T，β3=(1 1 —6)T，试求坐标变换公式．请帮忙给出正确答案和分析，谢谢！
设a1 a2线性相关 b1 b2也线性相关 问a1+b1 a2+b2是否一定线性相关?试举例说明之．
设a1，a2线性相关，b1，b2也线性相关，问a1+b1，a2+b2是否一定线性相关?试举例说明之．请帮忙给出正确答案和分析，谢谢！
若1 kg的力能使弹簧伸长1 cm 问要使这弹簧伸长10 cm需做多少功?请帮忙给出正确答案和分析
若1 kg的力能使弹簧伸长1 cm，问要使这弹簧伸长10 cm需做多少功?请帮忙给出正确答案和分析，谢谢！
