求一个正交变换化下列二次型成标准形： (1)f=2x12+3x22+3x32+4x2x3； (2)f

正确答案：(1)二次型f的矩阵为A=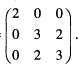它的特征多项式为 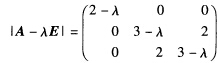=(2一λ)[(3一λ)²一4 =(2一λ)(5一λ)(1一λ)于是A的特征值为λ₁=2λ₂=5λ₃=1．对应特征值λ₁=2解方程(A一2E)x=0由对应特征值λ₂=5解方程(A一5E)x=0由对就特征值λ₃=1解方程(A—E)x=0由且标准形为 f=2y₁²+5y₂²+y₃²．(2)二次型的矩阵为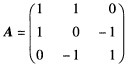它的特征多项式为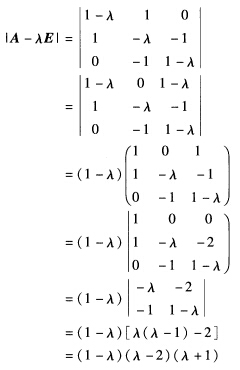于是A的特征值为λ₁=一1λ₂=1λ₃=2．①对应特征值λ₁=一1解方程(A+E)x=0得基础解系 ξ₁=[一121^T将其单位化得 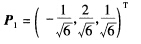②对应特征值λ₂=1解方程(A一E)x=0得基础解系 ξ₂=[101^T将单位化得 ③对应特征值λ₃=2解方程(A一2E)x=0得基础解系 ξ₃=[一1一11^T．将其单位化得 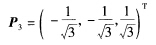于是所求的正交变换为 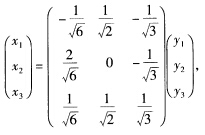且标准形为f=一y₁²+y₂²+2y₃²．
(1)二次型f的矩阵为A=它的特征多项式为=(2一λ)[(3一λ)2一4=(2一λ)(5一λ)(1一λ),于是A的特征值为λ1=2,λ2=5,λ3=1．对应特征值λ1=2,解方程(A一2E)x=0,由对应特征值λ2=5,解方程(A一5E)x=0,由对就特征值λ3=1,解方程(A—E)x=0,由且标准形为f=2y12+5y22+y32．(2)二次型的矩阵为它的特征多项式为于是A的特征值为λ1=一1,λ2=1,λ3=2．①对应特征值λ1=一1,解方程(A+E)x=0得基础解系ξ1=[一1,2,1T,将其单位化,得②对应特征值λ2=1,解方程(A一E)x=0得基础解系ξ2=[1,0,1T,将单位化,得③对应特征值λ3=2,解方程(A一2E)x=0得基础解系ξ3=[一1,一1,1T．将其单位化,得于是,所求的正交变换为且标准形为f=一y12+y22+2y32．