一个飞轮以每分钟1500转的转速作逆时针转动．制动后 飞轮均匀地减速 经50s而停止转动．求：(1)
一个飞轮以每分钟1500转的转速作逆时针转动．制动后，飞轮均匀地减速，经50s而停止转动．求：(1)角加速度a；(2)从开始制动到静止，飞轮转过的圈数N；(3)制动开始后t=25s时飞轮的角速度ω；(4)设飞轮半径为1m，求t=25s时飞轮边缘上一点的速度和加速度．
请帮忙给出正确答案和分析，谢谢！
参考解答
481***100
2024-11-04 04:32:10
正确答案：(1)如图5-1所示设初角速度为ω0则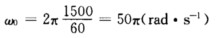
在t=50s时末角速度ω=0．所以角加速度为
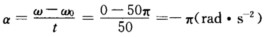(2)从开始制动到停止飞轮的角位移△θ及转数N分别为
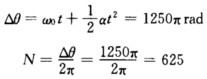(3)在t=25s时飞轮的角速度为 ω=ω0+at=78．6 rad·s-1 (4)在t=25s时飞轮边缘上一点的速度v其方向如图5-1所示其大小为 v=rω=25πm·-1相应的切向加速度和法向加速度分别为 Aτ=ra=-πm·s-2 an=rω2=(25π)2m·s-2该点的加速度为 a=aτ+an其方向如图5-1所示大小为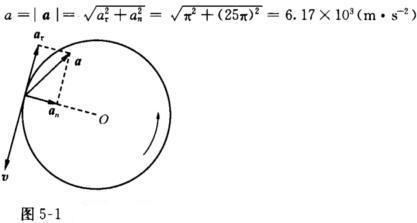
①角量ω、α都是矢量，ω的方向由右手螺旋法则来确定．α的方向由定义来确定．对刚体的定轴转动，ω、a两矢量都是沿轴的方向，用正、负即可描述方向．②本题是按定义来计算有关的角量和线量的．如果已知角加速度a=a(t)和初始条件(即初始角速度ω0和初始角位置θ0)，用积分法即可求角速度ω和角坐标θ与时间的关系．
相似问题
如图5-7所示 A B为两个相同的绕着轻绳的定滑轮．A滑轮挂一个质量为M的物体 B滑轮受拉力F 而且
如图5-7所示，A、B为两个相同的绕着轻绳的定滑轮．A滑轮挂一个质量为M的物体，B滑轮受拉力F，而且F=Mg．设A、B两滑轮的角加速度分别为aA和aB．不计滑轮轴
如图(a)所示 质量为0．25kg的垒球被棒击中．在即将碰撞前以40m·s-1的速度水平飞行．被击中
如图(a)所示，质量为0．25kg的垒球被棒击中．在即将碰撞前以40m·s-1的速度水平飞行．被击中后球与水平方向成30°仰角返回，速率为60m·s-1．假设球与棒
波长为λ的平面简谐波以波速u沿X轴正方向传播。已知x=λ/2处质点的振动规律为（SI）。 （1）写出
波长为λ的平面简谐波以波速u沿X轴正方向传播。已知x=λ 2处质点的振动规律为（SI）。 （1）写出该平面简谐波的波动方程；（2）画出t=T时刻的波形图。请
一个半径为6m的圆台由电动机带动以10rad.min-1的转速绕通过圆台中心的铅直轴转动。一个人站在
一个半径为6m的圆台由电动机带动以10rad min-1的转速绕通过圆台中心的铅直轴转动。一个人站在圆台上，沿着圆台边缘相对于圆台以1 m s-1的速度走动，相对
有一列平面简谐波在介质中传播 波速u=100m·s-1．波线上右侧距波源O(坐标原点)为75．0m处
有一列平面简谐波在介质中传播，波速u=100m·s-1．波线上右侧距波源O(坐标原点)为75．0m处的一点P的运动方程为yP=0．30cos(2πt+ π 2)(SI)，求：(1)波
