氢原子定态问题的Schrodinger方程是 其中h μ Z e E都是常数 试在球坐标系下将方程
氢原子定态问题的Schrodinger方程是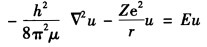 
其中h，μ，Z，e，E都是常数，试在球坐标系下将方程分离变量。
请帮忙给出正确答案和分析，谢谢！
参考解答
481***102
2024-11-17 20:54:55
正确答案：先令A=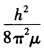
B=Ze2则Schrodinger方程可以简单写为
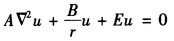由Laplace算符在球坐标下的表达式可知在球坐标下Schrodinger方程的表达式为
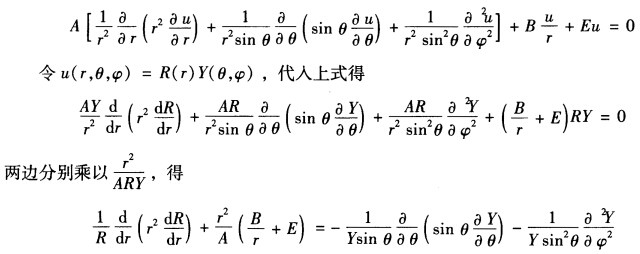要使上式成立则并有两边等于同一个常数记为ι(ι+1)从而
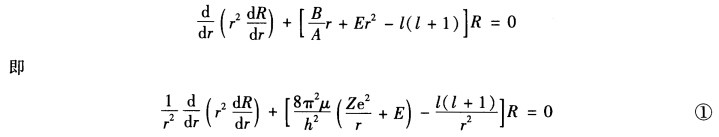至于Y则满足球谐函数方程
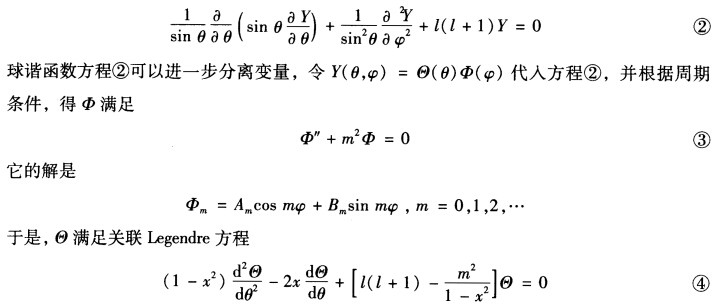其中x=cos θ。
先令A=,B=Ze2,则Schrodinger方程可以简单写为由Laplace算符在球坐标下的表达式可知,在球坐标下,Schrodinger方程的表达式为要使上式成立,则并有两边等于同一个常数,记为ι(ι+1),从而至于Y,则满足球谐函数方程其中x=cosθ。
相似问题
设α b∈R 证明：若对任何正数ε有｜α-b｜＜ε 则α=b。请帮忙给出正确答案和分析 谢谢！
设α，b∈R，证明：若对任何正数ε有｜α-b｜＜ε，则α=b。请帮忙给出正确答案和分析，谢谢！
将下列函数按勒让德多项式展开： (1)f(x)=x3 (2)f(x)=|x| 设有一个半径为a的均匀
将下列函数按勒让德多项式展开： (1)f(x)=x3 (2)f(x)=|x| 设有一个半径为a的均匀介质球，介电常设有一个半径为a的均匀介质球，介电常数为ε，在与球心
利用函数y=[x]求解： (1)某系各班级推选学生代表 每5人推选1名代表 余额满3人可增选1名．写
利用函数y=[x]求解： (1)某系各班级推选学生代表，每5人推选1名代表，余额满3人可增选1名．写出可推选代表数y与班级学生数x之间的函数关系(假设每班学生
将下列函数按勒让德多项式展开： (1)f(x)=x3 (2)f(x)=|x| 设有半径为a的导体球壳
将下列函数按勒让德多项式展开： (1)f(x)=x3 (2)f(x)=|x| 设有半径为a的导体球壳，被一层过球心设有半径为a的导体球壳，被一层过球心的水平的绝缘薄片
设f(x)为R上的单调函数 定义g(x)=f(x+0) 证明：g(x)在R上每一点都右连续。请帮忙给
设f(x)为R上的单调函数，定义g(x)=f(x+0)，证明：g(x)在R上每一点都右连续。请帮忙给出正确答案和分析，谢谢！
