举例说明下列各命题是错误的： (1)若向量组a1 a2 … am是线性相关的 则a1可由a2 … a

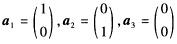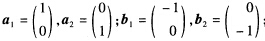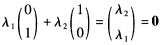正确答案：命题(1)是错误的反例：取向量则向量组a₁a₂a₃线性相关因它含有零向量．但a₁并不能由a₂a₃线性表示因为a₂a₃的任何的线性组合所得向量的第一个分量是零．命题(2)是错误的反例：取再取λ₁=λ₂=1则有λ₁a₁+λ₂a₂+λ₁b₁+λ₂b₂=0成立但a₁a₂线性无关；b₁b₂也线性无关．命题(3)是错误的反例：取此时若有λ₁a₁+λ₂a₂+λ₁b₁+λ₂b₂=成立只有λ₁=λ₂=0但向量组a₁a₂和向量组b₁b₂都线性相关．命题(4)是错误的反例：取则向量组a₁a₂和向量组b₁b₂均线性相关．但对此两向量组不存在不全为零的数λ₁λ₂使λ₁a₁+λ₂a₂=0和λ₁b₁+λ₂b₂=0同时成立因由上面第一式可得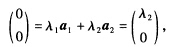 于是λ₂=0同理由第二式得λ₁=0．
命题(1)是错误的,反例：取向量则向量组a1,a2,a3线性相关,因它含有零向量．但a1并不能由a2,a3线性表示,因为a2,a3的任何的线性组合所得向量的第一个分量是零．命题(2)是错误的,反例：取再取λ1=λ2=1,则有λ1a1+λ2a2+λ1b1+λ2b2=0成立,但a1,a2线性无关；b1,b2也线性无关．命题(3)是错误的,反例：取此时若有λ1a1+λ2a2+λ1b1+λ2b2=成立,只有λ1=λ2=0,但向量组a1,a2和向量组b1,b2都线性相关．命题(4)是错误的,反例：取则向量组a1,a2和向量组b1,b2均线性相关．但对此两向量组不存在不全为零的数λ1,λ2使λ1a1+λ2a2=0和λ1b1+λ2b2=0同时成立,因由上面第一式可得于是λ2=0,同理由第二式得λ1=0．