设矩阵A=(a1 a2 a3 a4) 其中a2 a3 a4线性无关 a1=2a2一a3；向量b=a1

正确答案：显然这是一个四元方程．先决定系数矩阵A的秩． 因a₂a₃a₄线性无关故R(A)≥3；又因a₁能由a₂a₃线性表示 a₁a₂a₃线性相关 a₁a₂a₃a₄线性相关(部分相关则整体相关) R(A)≤3．综合上面两个不等式有R(A)=3从而原方程的基础解系所含向量个数为4—3=1．进一步a₁=2a₂一a₃a₂+a₃=0x=(1一210)^T是导出组Ax=0的解x=(1一210)^T是导出组的基础解系；又 b=a₁+a₂+a₃+a₄x=(1111)^T方程Ax=b的解于是由非齐次线性方程解的结构定理原方程的通解为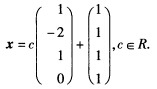
显然,这是一个四元方程．先决定系数矩阵A的秩．因a2,a3,a4线性无关,故R(A)≥3；又因a1能由a2,a3线性表示a1,a2,a3线性相关a1,a2,a3,a4线性相关(部分相关则整体相关)R(A)≤3．综合上面两个不等式,有R(A)=3,从而原方程的基础解系所含向量个数为4—3=1．进一步,a1=2a2一a3,a2+a3=0x=(1,一2,1,0)T是导出组Ax=0的解x=(1,一2,1,0)T是导出组的基础解系；又b=a1+a2+a3+a4,x=(1,1,1,1)T方程Ax=b的解,于是由非齐次线性方程解的结构定理,原方程的通解为