求一个齐次线性方程 使它的基础解系为 ξ1=(0 1 2 3)T ξ2=(3 2 1 0)T.请帮
求一个齐次线性方程,使它的基础解系为 ξ1=(0,1,2,3)T, ξ2=(3,2,1,0)T.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:具体计算如下: 取基础解系为 η1T=(1一210)η2T=(2一301).故A可取为
取基础解系为 η1T=(1一210)η2T=(2一301).故A可取为 对应方程组为
对应方程组为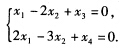
具体计算如下:取基础解系为η1T=(1,一2,1,0),η2T=(2,一3,0,1).故A可取为对应方程组为
相似问题
设在区间[0 1]上f(x)>0 则f(0) f(1) f(1)-f(0)或f(0)-f(1)的大小
设在区间[0,1]上f(x)>0,则f(0),f(1),f(1)-f(0)或f(0)-f(1)的大小顺序是( ).A.f"(1)>f"(0)>f(1)-f(0)B.f"(1)>f(1)-f(0)>f"(0)C.f(1)-f(0)>
函数f(x)=xsinx( ).A.当x→∞时为无穷大B.在(-∞ +∞)内有界C.在(-∞ +∞)
函数f(x)=xsinx( ).A.当x→∞时为无穷大B.在(-∞,+∞)内有界C.在(-∞,+∞)内无界D.在x→∞时有有限极限请帮忙给出正确答案和分析,谢谢!
验证a1=(1 一1 0)T a2=(2 1 3)T a3=(3 1 2)T为R3的一个基 并把v1
验证a1=(1,一1,0)T,a2=(2,1,3)T,a3=(3,1,2)T为R3的一个基,并把v1=(5,0,7)T,v2=(一9,一8,一13)T用这个基线性表示.请帮忙给出正确答案和分析,谢谢!
在某国 每年有比例为p的农村居民移居城镇 有比例为q的城镇居民移居农村.假设该国总人口数不变 且上述
在某国,每年有比例为p的农村居民移居城镇,有比例为q的城镇居民移居农村.假设该国总人口数不变,且上述人口迁移的规律也不变.把n年后农村人口和城镇人
已知α1 α2 α3是齐次线性方程组Ax=0的一个基础解系 证明α1+α2 α2+α3 α3+α1也
已知α1,α2,α3是齐次线性方程组Ax=0的一个基础解系,证明α1+α2,α2+α3,α3+α1也是该方程组的一个基础解系.请帮忙给出正确答案和分析,谢谢!












