已知α1 α2 α3是齐次线性方程组Ax=0的一个基础解系 证明α1+α2 α2+α3 α3+α1也

正确答案：由 A(α₁+α₂)=Aα₁+Aα₂=0+0=0知α₁+α₂是齐次方程组Ax=0的解．类似可知α₂+α₃α₃+α₁也是Ax=0的解． 若 k₁(α₁+α₂)+k₂(α₂+α₃)+k₃(α₃+α₁)=0 即 (k₁+k₃)α₁+(k₁+k₂)α₂+(k₂+k₃)α₃=0． 因为α₁α₂α₃是基础解系它们是线性无关的故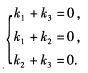由于此方程组系数行列式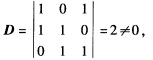故必有k₁=k₂=k₃=0所以α₁+α₂α₂+α₃α₃+α₁是方程组Ax=0的基础解系．
由A(α1+α2)=Aα1+Aα2=0+0=0知,α1+α2是齐次方程组Ax=0的解．类似可知α2+α3,α3+α1也是Ax=0的解．若k1(α1+α2)+k2(α2+α3)+k3(α3+α1)=0,即(k1+k3)α1+(k1+k2)α2+(k2+k3)α3=0．因为α1,α2,α3是基础解系,它们是线性无关的,故由于此方程组系数行列式故必有k1=k2=k3=0,所以α1+α2,α2+α3,α3+α1是方程组Ax=0的基础解系．