构造适当的概率模型 证明下列等式(n≥m≥1)： 请帮忙给出正确答案和分析 谢谢！
构造适当的概率模型，证明下列等式(n≥m≥1)：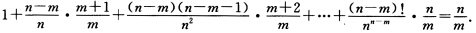 
请帮忙给出正确答案和分析，谢谢！
参考解答
470***445
2023-11-14 12:54:33
正确答案：两边乘
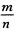将等式化为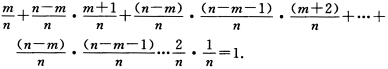
设一袋中有m个白球n一m个黑球从其中一次一次地取球．如果取出的是黑球就放入一个白球直到取得白球为止．若用Ai(i=12…n一m+1)表示第i次才取得白球则A1A2…An—m+1互不相容且A1∪A2∪…∪An—m+1=S因而P(A1)+P(A2)+…+P(An—m+1)=1．容易算得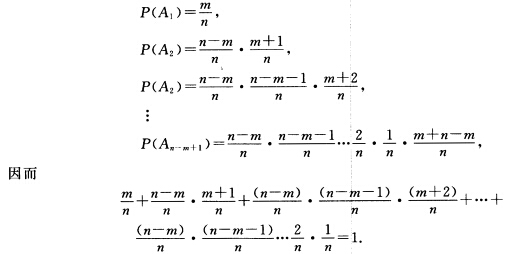
两边同乘，等式化为从第一项，可以看到这像一个袋中有n个球，其中有m个白球，n一m个黑球，任取一球为白球的概率．从第二项*看，好像是第一次取得黑球，第二次取得白球的概率．不过第二个因子的分子为m+1，应当是第一次取出黑球后要放入袋中一个白球，再取第二个球，以此取球模型分析其他各项是吻合的．这一模型是设袋中有m个白球，n—m个黑球，从其中一次一次地取球．如果取出的是黑球，就放入一个白球，直到取出白球为止．在此模型中，迟早取到白球的概率为1，这就是所要证明的等式．
相似问题
户籍改革的底线是不能降低对城市居民的既得公共服务及福利水平。()判断对错
户籍改革的底线是不能降低对城市居民的既得公共服务及福利水平。()判断对错
设只有一个泊位的码头有甲 乙两艘船停靠 二船各自可能在一昼夜的任何时刻到达．设两艘船停靠的时间分别为
设只有一个泊位的码头有甲、乙两艘船停靠，二船各自可能在一昼夜的任何时刻到达．设两艘船停靠的时间分别为1小时和2小时，求下列事件的概率： A1：码头
是否存在2次多项式f(x)=ax2+bx+c其图象经过下述4个点：P(1 2) Q(一1 3) M(
是否存在2次多项式f(x)=ax2+bx+c其图象经过下述4个点：P(1，2)，Q(一1，3)，M(一4，5)，N(0，2)．请帮忙给出正确答案和分析，谢谢！
一批产品共100件 其中5件是次品．抽样检查时 每次任取其中一件检查 如果是次品 就认为这批产品不合
一批产品共100件，其中5件是次品．抽样检查时，每次任取其中一件检查，如果是次品，就认为这批产品不合格而拒绝接受．如果是合格品，则再抽查一件，检查
从0 1 2 … 9这10个数字中任取1个 假定每个数字都以1／10的概率被取到 取后放回 先后取了
从0，1，2，…，9这10个数字中任取1个，假定每个数字都以1／10的概率被取到，取后放回，先后取了6个数字，则6个数字中至少有两个相同的概率为( )．A．0
