设随机变量X在(一l l)(l＞0)上均匀分布 且方程 4x2+4Xx+X+2=0 有实根的概率为
设随机变量X在(一l，l)(l＞0)上均匀分布，且方程 4x2+4Xx+X+2=0 有实根的概率为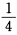
，求X的概率密度．
请帮忙给出正确答案和分析，谢谢！
参考解答
470***444
2023-11-14 03:52:26
正确答案：为使方程 4x2+4Xx+X+2=0有实根的充要条件是 16X2一16(X+2)≥0即X2一X一2≥0 解此不等式得X≤一1或X≥2．若用A表示事件“方程有实根”则A={X≤一1)∪{X≥2)P(A)=P{X≤一1)+P{X≥2． 显然当0＜l≤1时要使P(A)=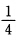
是不可能的．考虑1＜l＜2此时 
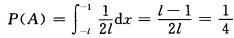解得l=2．考虑l≥2此时 
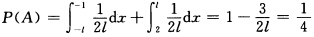解得l=2．因此当l=2时X的概率密度为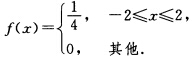 
为使方程4x2+4Xx+X+2=0有实根的充要条件是16X2一16(X+2)≥0,即X2一X一2≥0,解此不等式得X≤一1或X≥2．若用A表示事件“方程有实根”,则A={X≤一1)∪{X≥2),P(A)=P{X≤一1)+P{X≥2．显然,当0＜l≤1时,要使P(A)=是不可能的．考虑1＜l＜2,此时,解得l=2．考虑l≥2,此时,解得l=2．因此当l=2时,X的概率密度为
相似问题
下列四个函数中 可以是某个随机变量的概率密度的是( )． 请帮忙给出正确答案和分析 谢谢！
下列四个函数中，可以是某个随机变量的概率密度的是( )． 请帮忙给出正确答案和分析，谢谢！
设离散型随机变量X的分布函数为 且P{X=2}= 则(a b}=( )． 请帮忙给出正确答案和分
设离散型随机变量X的分布函数为 且P{X=2}=，则(a，b}=( )． 请帮忙给出正确答案和分析，谢谢！
某射击小组共有20名射手 其中一级射手4人 二级射手8人 三级射手7人 四级射手1人．一 二 三 四
某射击小组共有20名射手，其中一级射手4人，二级射手8人，三级射手7人，四级射手1人．一、二、三、四级射手能通过选拔进入比赛的概率分别为0．9，0．7，0
一盒中有10个产品 其中有4个次品 6个正品 随机地抽取一个测试 测试后不放回 直到次品都找到．求最
一盒中有10个产品，其中有4个次品，6个正品，随机地抽取一个测试，测试后不放回，直到次品都找到．求最后一个次品在下列情况发现的概率： (1)在第5次测
表示下列随机试验的随机事件 并分析它们之间的相互关系： (1)掷一颗骰子 记录掷得的点数 考虑事件：
表示下列随机试验的随机事件，并分析它们之间的相互关系： (1)掷一颗骰子，记录掷得的点数，考虑事件：“掷得的点数不超过2”，“掷得的点数不超过3”，
